题目内容
6.已知α,β为锐角,cosα=$\frac{1}{7},sin(α+β)=\frac{{5\sqrt{3}}}{14}$,则cosβ=$\frac{1}{2}$.分析 由条件利用同角三角函数的基本关系求得sinα、cos(α+β)的值,再利用两角差的三角公式求得cosβ=cos[(α+β)-α]的值.
解答 解:∵α,β为锐角,cosα=$\frac{1}{7}$<$\frac{1}{2}$,∴α>$\frac{π}{3}$,sinα=$\frac{4\sqrt{3}}{7}$.
又 sin(α+β)=$\frac{5\sqrt{3}}{14}$,∴α+β 为钝角,∴cos(α+β)=-$\sqrt{{1-sin}^{2}(α+β)}$=-$\frac{11}{14}$,
∴cosβ=cos[(α+β)-α]=cos(α+β)cosα+sin(α+β)sinα=-$\frac{11}{14}$•$\frac{1}{7}$+$\frac{5\sqrt{3}}{14}$•$\frac{4\sqrt{3}}{7}$=$\frac{1}{2}$,
故答案为:$\frac{1}{2}$.
点评 本题主要考查同角三角函数的基本关系,两角差的三角公式的应用,属于基础题.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
11.函数g(x)是奇函数f(x)(x∈R)的导函数,f(1)=0,当x>0时,xg(x)-f(x)<0,则使得f(x)<0成立的x的取值范围是( )
| A. | (-∞,-1)∪(0,1) | B. | (0,1)∪(1,+∞) | C. | (-∞,-1)∪(-1,0) | D. | (-1,0)∪(1,+∞) |
16.若$\sqrt{x}+\sqrt{y}≤a\sqrt{x+y}$(x>0,y>0)恒成立,则a的最小值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 2$\sqrt{2}$ |
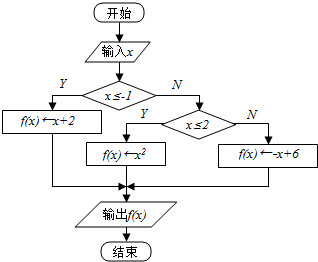 根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).
根据流程图,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是(-∞,0)∪(1,4).