题目内容
(12分)已知直线![]() ,
,![]() 圆C:
圆C:![]() ,
,![]() ;
;
![]() (Ⅰ)证明直线
(Ⅰ)证明直线![]() 与圆C总相交;
与圆C总相交;
![]() (Ⅱ)若圆C上存在两点关于
(Ⅱ)若圆C上存在两点关于![]() 对称,求
对称,求![]() 的值;
的值;
解析:(1)由![]() 得:
得:![]()
令![]()
![]()
![]() ,所以
,所以![]() 过定点
过定点![]()
![]() ,所以
,所以![]() 点在圆内,所以直线
点在圆内,所以直线![]() 与圆C相交 ………………3分
与圆C相交 ………………3分
(2)直线![]() 过圆C的圆心,(0,0)点代入得,
过圆C的圆心,(0,0)点代入得,![]() ………………6分
………………6分
(3)由题意得![]() ,
,![]()
![]() ① ………………8分
① ………………8分
![]() 设
设![]() 点关于
点关于![]() 对称点为
对称点为![]() ,则
,则
![]() ,所以直线
,所以直线![]() 的方程为:
的方程为:![]() ②
②

练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
 与曲线
与曲线

 交于不同的两点
交于不同的两点 ,
, 为坐标原点.
为坐标原点. ,求证:曲线
,求证:曲线 是一个圆;
是一个圆; ,当
,当 且
且 时,求曲线
时,求曲线 的取值范围.
的取值范围. 过椭圆
过椭圆 的右焦点
的右焦点 ,抛物线:
,抛物线: 的焦点为椭圆
的焦点为椭圆 的上顶点,且直线
的上顶点,且直线 交椭圆
交椭圆 、
、 两点,点
两点,点 上的射影依次为点
上的射影依次为点 、
、 、
、 .
. ,且
,且 ,当
,当 变化时,探求
变化时,探求 的值是否为定值?若是,求出
的值是否为定值?若是,求出 、
、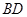 ,试探索当
,试探索当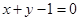 与椭圆
与椭圆 相交于
相交于 、
、 两点,
两点,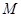 是线段
是线段 上
上 ,且点M在直线
,且点M在直线 上,
上, 的对称点在单位圆
的对称点在单位圆 上,求椭圆的方程。
上,求椭圆的方程。