题目内容
已知R为全集,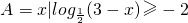 ,
,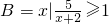 ,则(CRA)∩B是
,则(CRA)∩B是
- A.{x|-2<x≤-1或 x=3}
- B.{x|-2<x<-1或 x=3}
- C.{x|-1<x<3或 x=-2}
- D.{x|-1<x≤3或 x=-2}
B
分析:利用对数函数的性质求解集合A,分式不等式求解集合B,然后求出A的补集与集合B的交集.
解答:A={x|lo (3-x)≥-2}={x|1≤x<3};
(3-x)≥-2}={x|1≤x<3};
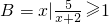 ={x|-2<x≤3};
={x|-2<x≤3};
所以CRA={x|x<1或x≥3},
所以(CRA)∩B={x|x<1或x≥3}∩{x|-2<x≤3}={x|-2<x<-1或 x=3};
故选B.
点评:本题考查对数函数的单调性,分式不等式的求法,集合的基本运算.
分析:利用对数函数的性质求解集合A,分式不等式求解集合B,然后求出A的补集与集合B的交集.
解答:A={x|lo
 (3-x)≥-2}={x|1≤x<3};
(3-x)≥-2}={x|1≤x<3};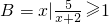 ={x|-2<x≤3};
={x|-2<x≤3};所以CRA={x|x<1或x≥3},
所以(CRA)∩B={x|x<1或x≥3}∩{x|-2<x≤3}={x|-2<x<-1或 x=3};
故选B.
点评:本题考查对数函数的单调性,分式不等式的求法,集合的基本运算.

练习册系列答案
相关题目
已知R为全集,A={x|log
(3-x)≥-2},B={y|y=2x,x∈R},则(CRA)∩B=( )
| 1 |
| 2 |
| A、φ |
| B、(0,+∞) |
| C、(-∞,-1)∪(0,+∞) |
| D、[3,+∞) |
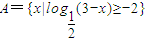 ,
,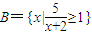 ,则(CRA)∩B是( )
,则(CRA)∩B是( )