题目内容
 棱长为a的正方体A1B1C1D1-ABCD中,O为面ABCD的中心.
棱长为a的正方体A1B1C1D1-ABCD中,O为面ABCD的中心.(1)求证:AC1⊥平面B1CD1;
(2)求四面体OBC1D1的体积;
(3)线段AC上是否存在P点(不与A点重合),使得A1P∥面CC1D1D?如果存在,请确定P点位置,如果不存在,请说明理由.
分析:(1)利用正方体的性质可得AB⊥B1C,由正方形的性质可得B1C⊥BC1.再利用线面垂直的判定可得B1C⊥AC1,同理可得AC1⊥CD1,利用线面垂直的判定定理即可证明结论;
(2))由CC1∥平面BB1D1D,可得点C1到平面BOD1的距离与点C到此平面的距离相等,利用“等体积变形”即可得到∴V四面体OBC1D1=VC1-BOD1=VC-BOD1,利用三棱锥的体积计算公式即可得出.
(3)利用面面平行的性质即可得出结论.
(2))由CC1∥平面BB1D1D,可得点C1到平面BOD1的距离与点C到此平面的距离相等,利用“等体积变形”即可得到∴V四面体OBC1D1=VC1-BOD1=VC-BOD1,利用三棱锥的体积计算公式即可得出.
(3)利用面面平行的性质即可得出结论.
解答:(1)证明:由正方体可得AB⊥平面BCC1B1,
∴AB⊥B1C.
由正方形BCC1B1可得B1C⊥BC1.
而AB∩BC1=B,∴B1C⊥平面ABC1,
∴B1C⊥AC1.
同理可证,CD1⊥AC1,
又CB1∩CD1=C,∴AC1⊥平面B1CD1;
(2)∵CC1∥平面BB1D1D,∴点C1到平面BOD1的距离与点C到此平面的距离相等,
∴V四面体OBC1D1=VC1-BOD1=VC-BOD1=
S△BOD1×OC=
×
×
×a×
=
.
(3)由正方体可得平面ABB1A1∥平面CC1D1D,故过点A1与平面CC1D1D平行的直线只能在平面ABB1A1内,
因此在线段AC上除了点A外不存在其它点P,使得A1P∥面CC1D1D.
∴AB⊥B1C.
由正方形BCC1B1可得B1C⊥BC1.
而AB∩BC1=B,∴B1C⊥平面ABC1,
∴B1C⊥AC1.
同理可证,CD1⊥AC1,
又CB1∩CD1=C,∴AC1⊥平面B1CD1;
(2)∵CC1∥平面BB1D1D,∴点C1到平面BOD1的距离与点C到此平面的距离相等,
∴V四面体OBC1D1=VC1-BOD1=VC-BOD1=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| ||
| 2 |
| a3 |
| 12 |
(3)由正方体可得平面ABB1A1∥平面CC1D1D,故过点A1与平面CC1D1D平行的直线只能在平面ABB1A1内,
因此在线段AC上除了点A外不存在其它点P,使得A1P∥面CC1D1D.
点评:熟练掌握方体的性质、正方形的性质、线面垂直的判定和性质定理、线面平行的性质定理、“等体积变形”、三棱锥的体积计算公式、面面平行的性质定理是解题的结论.

练习册系列答案
相关题目
在棱长为a的正方体ABCD-A1B1C1D1中,M是AA1的中点,则点A1到平面MBD的距离是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为棱AA1与CC1的中点,求四棱锥的A1-EBFD1的体积.
如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别为棱AA1与CC1的中点,求四棱锥的A1-EBFD1的体积. 如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的:
如图是从上下底面处在水平状态下的棱长为a的正方体ABCD-A1B1C1D1中分离出来的: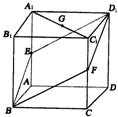 如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别是棱AA1和CC1的中点,G是A1C1的中点,求:
如图,已知ABCD-A1B1C1D1是棱长为a的正方体,E、F分别是棱AA1和CC1的中点,G是A1C1的中点,求: