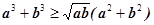题目内容
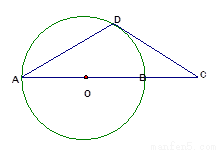
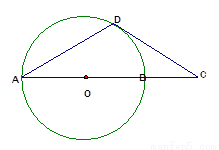
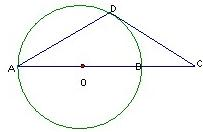 9、AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证:AB=2BC.
9、AB是⊙O的直径,D为⊙O上一点,过点D作⊙O的切线交AB延长线于C,若DA=DC,求证:AB=2BC.分析:证法一、可以连接OD,构造直角三角形,然后求出∠DCO,然后根据30°所对的直角边等于斜边的一半,得出结论;
证法二、连接OD,DB,再证明△ADB≌△CDO,得到AB=OC,转化为证明CO=2BC
证法二、连接OD,DB,再证明△ADB≌△CDO,得到AB=OC,转化为证明CO=2BC
解答: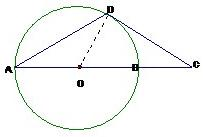 证明:法一:连接OD,则:OD⊥DC,
证明:法一:连接OD,则:OD⊥DC,
又OA=OD,DA=DC,
所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=30°,∠DOC=60°,
所以OC=2OD,
即OB=BC=OD=OA,
所以AB=2BC.
证法二:连接OD、BD.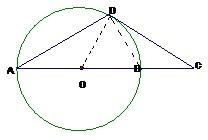
因为AB是圆O的直径,所以∠ADB=90°,
AB=2OB.
因为DC是圆O的切线,所以∠CDO=90°.
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO.
即2OB=OB+BC,得OB=BC.故AB=2BC.
 证明:法一:连接OD,则:OD⊥DC,
证明:法一:连接OD,则:OD⊥DC,又OA=OD,DA=DC,
所以∠DAO=∠ODA=∠DCO,
∠DOC=∠DAO+∠ODA=2∠DCO,
所以∠DCO=30°,∠DOC=60°,
所以OC=2OD,
即OB=BC=OD=OA,
所以AB=2BC.
证法二:连接OD、BD.

因为AB是圆O的直径,所以∠ADB=90°,
AB=2OB.
因为DC是圆O的切线,所以∠CDO=90°.
又因为DA=DC,所以∠DAC=∠DCA,
于是△ADB≌△CDO,从而AB=CO.
即2OB=OB+BC,得OB=BC.故AB=2BC.
点评:本题考查的知识点是切线的性质,即切线垂直过切点的半径,将问题转化为直角三角形问题,解直角三角形即可得到答案.

练习册系列答案
相关题目
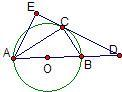 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.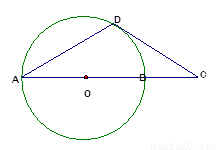
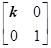 ,N=
,N=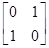 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
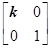 ,N=
,N=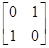 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值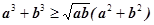
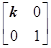 ,N=
,N=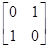 ,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值
,点A、B、C在矩阵MN对应的变换下得到点A1,B1,C1,△A1B1C1的面积是△ABC面积的2倍,求实数k的值