题目内容
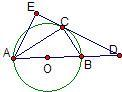 如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.
如图,已知⊙O是△ABC的外接圆,AB是⊙O的直径,D是AB延长线上一点,AE⊥DC交DC的延长线于点E,且AC平分∠EAB.(1)求证:DE是⊙O的切线;
(2)若AB=6,AE=
| 24 | 5 |
分析:(1)要证DE是⊙O的切线,只要连接OC,再证∠DCO=90°即可.
(2)已知两边长,求其它边的长,可以来三角形相似,对应边成比例来求.
(2)已知两边长,求其它边的长,可以来三角形相似,对应边成比例来求.
解答: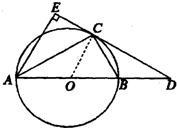 (1)证明:连接OC
(1)证明:连接OC
∵AC平分∠EAB
∴∠EAC=∠BAC
又在圆中OA=OC
∴∠AC0=∠BAC
∴∠EAC=∠ACO
∴OC∥AE(内错角相等,两直线平行)
则由AE⊥DC知
OC⊥DC
即DE是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°
∴△DCO∽△DEA
∴BD=2
∵Rt△EAC∽Rt△CAB.
∴AC2=
由勾股定理得
BC=
.
 (1)证明:连接OC
(1)证明:连接OC∵AC平分∠EAB
∴∠EAC=∠BAC
又在圆中OA=OC
∴∠AC0=∠BAC
∴∠EAC=∠ACO
∴OC∥AE(内错角相等,两直线平行)
则由AE⊥DC知
OC⊥DC
即DE是⊙O的切线.
(2)∵∠D=∠D,∠E=∠OCD=90°
∴△DCO∽△DEA
∴BD=2
∵Rt△EAC∽Rt△CAB.
∴AC2=
| 144 |
| 5 |
由勾股定理得
BC=
6
| ||
| 5 |
点评:本题考查了切线的判定、相似三角形的性质和勾股定理的运用.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
相关题目
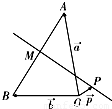
 如图,已知O、A、B是平面上三点,向量
如图,已知O、A、B是平面上三点,向量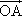 =a,
=a,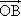 =b,
=b,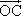 =c,且|a|=2,|b|=1,|c|=3,试用a和b表示c.
=c,且|a|=2,|b|=1,|c|=3,试用a和b表示c.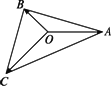
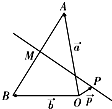 如图,已知O、A、B是平面上三点,向量
如图,已知O、A、B是平面上三点,向量 =
= ,
, =
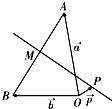
= .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量 =
= ,且|
,且| )的值是
)的值是



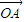 =
=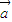 ,
,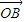 =
=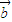 .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量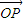 =
=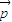 ,且|
,且|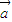 |=3,|
|=3,|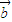 |=2,则
|=2,则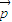 •(
•(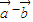 )的值是( )
)的值是( )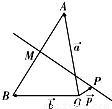




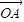 =
=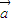 ,
,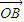 =
=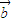 .在平面AOB上,P是线段AB垂直平分线上任意一点,向量
.在平面AOB上,P是线段AB垂直平分线上任意一点,向量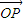 =
=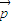 ,且|
,且|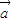 |=3,|
|=3,|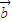 |=2,则
|=2,则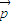 •(
•(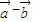 )的值是( )
)的值是( )