题目内容
设△ABC的内角A，B，C成等差数列，且满足条件sinAcosC=cos（120°-C）sinC，试判断△ABC的形状，并证明你的结论．
△ABC为等边三角形，理由为：
证明：∵△ABC的内角A，B，C成等差数列，
∴A+C=2B，又A+B+C=180°，
∴B=60°，A+C=120°，
∴sinAcosC=cos（120°-C）sinC变形为sinAcosC=cosAsinC，即sin（A-C）=0，
∵-π＜A-C＜π，∴A=C，
∴A=B=C=60°，
则△ABC为等边三角形．
证明：∵△ABC的内角A，B，C成等差数列，
∴A+C=2B，又A+B+C=180°，
∴B=60°，A+C=120°，
∴sinAcosC=cos（120°-C）sinC变形为sinAcosC=cosAsinC，即sin（A-C）=0，
∵-π＜A-C＜π，∴A=C，
∴A=B=C=60°，
则△ABC为等边三角形．
练习册系列答案
相关题目
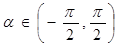，求使sin 
=
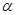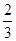成立的
= 
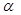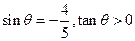，则
.