题目内容
若不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则实数a取值的集合
- A.{a|a≤2}
- B.{a|-2<a<2}
- C.{a|-2<a≤2}
- D.{a|a≤-2}
C
分析:先对二次项的系数a-2分类讨论,进而利用一元二次不等式的解法解出即可.
解答:①a=2时,不等式化为-4<0对一切x∈R恒成立,因此a=2满足题意;
②a≠2时,要使不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则必有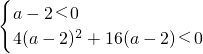 解得-2<a<2.
解得-2<a<2.
综上①②可知:实数a取值的集合是{a|-2<a≤2}.
故选C.
点评:熟练掌握一元二次不等式的解法和分类讨论的思想方法是解题的关键.
分析:先对二次项的系数a-2分类讨论,进而利用一元二次不等式的解法解出即可.
解答:①a=2时,不等式化为-4<0对一切x∈R恒成立,因此a=2满足题意;
②a≠2时,要使不等式(a-2)x2+2(a-2)x-4<0对一切x∈R恒成立,则必有
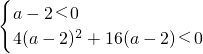 解得-2<a<2.
解得-2<a<2.综上①②可知:实数a取值的集合是{a|-2<a≤2}.
故选C.
点评:熟练掌握一元二次不等式的解法和分类讨论的思想方法是解题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目