题目内容
在边长为2的正方体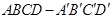 中,E 是BC的中点,F 是
中,E 是BC的中点,F 是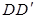 的中点
的中点
(Ⅰ)求证:CF ∥平面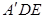
(Ⅱ)求二面角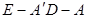 的平面角的余弦值。
的平面角的余弦值。
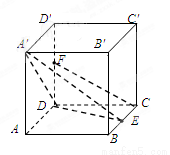
【答案】
1)证明:取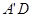 的中点记为G,连接GF、GE,
的中点记为G,连接GF、GE,
因为E、F均为中点,所以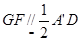 ,所以
,所以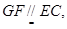
所以四边形FGEC是平行四边形,所以FC//GE,
又因为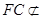 平面
平面 ,GE
,GE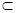 平面
平面 ,所以CF∥平面
,所以CF∥平面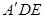
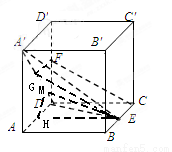
(2)取AD的中点H,连接HE,过H做HM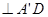 于M,连接ME,
于M,连接ME,
因为EH//AB,所以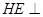 平面
平面 ,所以
,所以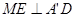 ,
,
所以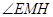 为二面角
为二面角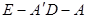 的平面角,
的平面角,
由EH=2,HM=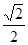 ,得
,得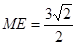 ,所以
,所以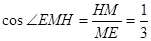 ,
,
所以二面角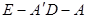 的平面角的余弦值为
的平面角的余弦值为 .
.
【解析】略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

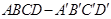 中,E是BC的中点,F是
中,E是BC的中点,F是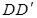 的中点
的中点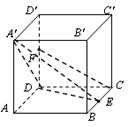
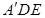
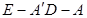 的平面角的余弦值.
的平面角的余弦值. 中,E是BC的中点, F是
中,E是BC的中点, F是 的中点
的中点
 的平面角的余弦值。
的平面角的余弦值。
 中,E是BC的中点,F是
中,E是BC的中点,F是 的中点
的中点
 的平面角的余弦值。
的平面角的余弦值。