题目内容
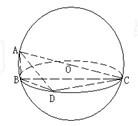 如图,球心到截面的距离为半径的一半,BC是截面圆的直径,D是圆周上一点,CA是球O的直径.
如图,球心到截面的距离为半径的一半,BC是截面圆的直径,D是圆周上一点,CA是球O的直径.(1)求证:平面ABD⊥平面ADC;
(2)如果球半径是
| 13 |
 |
| BC |
 |
| BD |
 |
| DC |
分析:(1)由已知中BC是截面圆的直径,D是圆周上一点,CA是球O的直径.由圆周角定理,可得CD⊥BD,CD⊥AD,由线面垂直的判定定理,可得CD⊥平面ABD,再由面面垂直的判定定理,即可得到平面ABD⊥平面ADC;
(2)根据球半径是
,D分
为两部分,且
:
=1:2,我们可以分别求出cos∠ACB,cos∠CBD,然后利用三余弦定理,即可得到答案.
(2)根据球半径是
| 13 |
 |
| BC |
 |
| BD |
 |
| DC |
解答:证明:(1)∵BC是截面圆的直径,D是圆周上一点,CA是球O的直径.
∴CD⊥BD,CD⊥AD,又由BD∩AD=D
∴CD⊥平面ABD,又由CD?平面ADC
∴平面ABD⊥平面ADC;
解:(2)∵球心到截面的距离为半径的一半,球半径AC=
,
则BC=
,∴cos∠ACB=
又∵D分
为两部分,且
:
=1:2,
∴cos∠CBD=
,
设AC与BD所成的角为θ,
由三余弦定理得:Cosθ=
则AC与BD所成的角为arccos
∴CD⊥BD,CD⊥AD,又由BD∩AD=D
∴CD⊥平面ABD,又由CD?平面ADC
∴平面ABD⊥平面ADC;
解:(2)∵球心到截面的距离为半径的一半,球半径AC=
| 13 |
则BC=
| 39 |
| ||
| 2 |
又∵D分
 |
| BC |
 |
| BD |
 |
| DC |
∴cos∠CBD=
| 1 |
| 2 |
设AC与BD所成的角为θ,
由三余弦定理得:Cosθ=
| ||
| 4 |
则AC与BD所成的角为arccos
| ||
| 4 |
点评:本题考查的知识点是平面与平面垂直的判定,异面直线及其所成的角,其中求平面的一条斜线与平面内一条直线的夹角时所用的三余弦定理是解答本题的关键.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
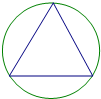 已知正四面体内接于半径为R的球,用一平面去截此正四面体和球,其截面如图,则球心到截面的距离为( )
已知正四面体内接于半径为R的球,用一平面去截此正四面体和球,其截面如图,则球心到截面的距离为( )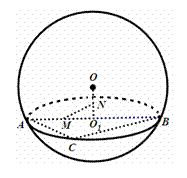 如图,用一平面去截球
如图,用一平面去截球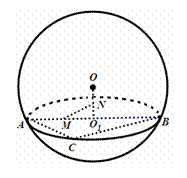 如图,用一平面去截球
如图,用一平面去截球 ,D分
,D分 为两部分,且
为两部分,且 ,求AC与BD所成的角.
,求AC与BD所成的角.