题目内容
13.设f(x)=4cos(ωx-$\frac{π}{6})sinωx-cos(2ωx+π),其中ω$sinωx-cos(2ωx+π),其中ω>0.(1)若最小正周期为π,求ω的值;
(2)在(1)的条件下,若不等式f(x)-m≥0对x∈$[{0,\frac{2π}{3}}]$都成立,求m的最大值.
(3)若f(x)在区间$[{-\frac{3π}{2},\frac{π}{2}}]$上为增函数,求ω的最大值.
分析 (1)由条件利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性求得ω的值.
(2)根据函数f(x)的解析式,利用正弦函数的定义域和值域,求得m的最大值.
(3)依题意知$[{-\frac{3π}{2},\frac{π}{2}}]⊆[{\frac{kπ}{ω}-\frac{π}{4ω},\frac{kπ}{ω}-\frac{π}{4ω}}]$,对某个k∈Z成立,故必有k=0,于是$\left\{\begin{array}{l}-\frac{3π}{2}≥-\frac{π}{4ω}\\ \frac{π}{2}≤\frac{π}{4ω}\end{array}\right.$,解得ω的最大值.
解答 解:(1)$f(x)=2\sqrt{3}sinωxcosωx+2{sin^2}ωx+cos2ωx$=$\sqrt{3}sin2ωx+1$,$T=\frac{2π}{2ω}=\frac{π}{ω}=π$,∴ω=1.
(2)由(1)得$f(x)=\sqrt{3}sin2x+1$,对于x∈$[{0,\frac{2π}{3}}]$,∴$0≤2x≤\frac{4π}{3}$,∴$-\frac{{\sqrt{3}}}{2}≤sin2x≤1$,∴$-\frac{1}{2}≤f(x)≤\sqrt{3}+1$,
由题意得$m≤-\frac{1}{2}$,即m最大值为$-\frac{1}{2}$.
(3)因为y=sinx在每个闭区间$[{\;}\right.2kπ-\frac{π}{2},2kπ+\frac{π}{2}\left.{\;}](k∈Z)$上为增函数,
$f(x)=\sqrt{3}sin2ωx+1(ω>0)$在每个区间$[{\frac{kπ}{ω}-\frac{π}{4ω},\frac{kπ}{ω}+\frac{π}{4ω}}],(k∈Z)$上为增函数.
依题意知:$[{-\frac{3π}{2},\frac{π}{2}}]⊆[{\frac{kπ}{ω}-\frac{π}{4ω},\frac{kπ}{ω}-\frac{π}{4ω}}]$ 对某个k∈Z成立,
此时必有k=0,于是,$\left\{\begin{array}{l}-\frac{3π}{2}≥-\frac{π}{4ω}\\ \frac{π}{2}≤\frac{π}{4ω}\end{array}\right.$,解得$ω≤\frac{1}{6}$,
故ω的最大值为$\frac{1}{6}$.
点评 本题主要考查三角恒等变换,正弦函数的周期性、定义域和值域,正弦函数的单调性,属于中档题.

 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案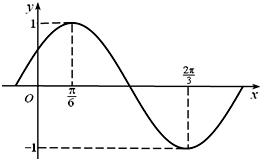 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)部分图象如图所示.