题目内容
若地球半径为R,在北纬45°圈上有A、B两点,且这两点间的球面距离为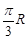 ,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
,则北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的余弦值为 ( )
(A)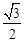 (B)
(B)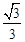 (C)
(C)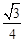 (D)
(D)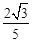
【答案】
B
【解析】A、B两点间的球面距离为以O为圆心,且过A,B的圆中弧AB的长度,
设∠AOB=α,则α•R=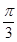 R,α=
R,α=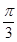 ,又OA=OB,∴△AOB为正三角形,∴AB=R.
,又OA=OB,∴△AOB为正三角形,∴AB=R.
设Q为北纬45°圈的圆心,则由球的截面圆形状可知,OQ⊥⊙Q面,∠OAQ=45°,
且截面圆半径长QA=R•cos∠OAQ=R•cos45°= 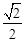 R.在△QAB中,
R.在△QAB中, 得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
得△QAB为等腰直角三角形.设M为AB中点,连接QM,OM,则OM⊥AB,QM⊥AB,
∴∠OMQ为北纬45°圈所在平面与过A、B两点的球的大圆面所成的二面角的平面角.
在RT△OMQ中,cos∠OMQ=QM/OM ==  ,所以所求二面角的余弦值是
,所以所求二面角的余弦值是 ,故选B.
,故选B.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目