题目内容
等差数列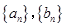 的前
的前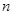 项和分别为
项和分别为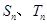 ,若
,若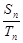 =
= ,则
,则 =_________
=_________
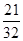
解析试题分析:等差数列的性质.∵在等差数列中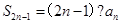 ,∴
,∴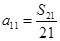 ,∴
,∴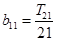 ,∴
,∴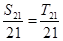 .又∵
.又∵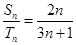 ,∴
,∴ =
=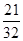 .
.
考点:1、等差数列的前 项和;2、等差数列的性质.
项和;2、等差数列的性质.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
题目内容
等差数列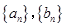 的前
的前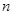 项和分别为
项和分别为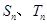 ,若
,若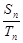 =
= ,则
,则 =_________
=_________
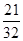
解析试题分析:等差数列的性质.∵在等差数列中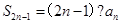 ,∴
,∴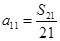 ,∴
,∴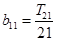 ,∴
,∴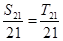 .又∵
.又∵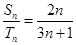 ,∴
,∴ =
=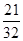 .
.
考点:1、等差数列的前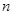 项和;2、等差数列的性质.
项和;2、等差数列的性质.

 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案