Question

过原点的直线l与双曲线y²-x²=1有两个交点，则直线l的斜率的取值范围为

1. A.
   （-1，1）
2. B.
   （-∞，-1）∪（1，+∞）
3. C.
   （-1，0）∪（0，1）
4. D.
   

Answer 1

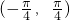
B
分析：先确定双曲线y²-x²=1的两条渐近线方程，再根据过原点的直线l与双曲线y²-x²=1有两个交点，可确定直线l的斜率的取值范围．
解答：双曲线y²-x²=1的两条渐近线方程为y=±x，其斜率分别为1，-1
要使过原点的直线l与双曲线y²-x²=1有两个交点，则直线l的斜率k必须满足k＞1，或k＜-1
∴直线l的斜率的取值范围为（-∞，-1）∪（1，+∞）
故选B．
点评：本题重点考查双曲线的性质，考查直线与双曲线的位置关系，求出双曲线的渐近线方程是解题的关键．