题目内容
本题有(1)、(2)、(3)三个选答题,每题7分,请考生任选2题作答,满分14分.如果多做,则按所做的前两题记分.作答时,先用2B铅笔在答题卡上把所选题目对应的题号涂黑,并将所选题号填入括号中.作
(1)选修4—2:矩阵与变换
若二阶矩阵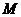 满足
满足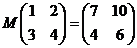 .
.
(Ⅰ)求二阶矩阵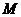 ;
;
(Ⅱ)把矩阵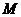 所对应的变换作用在曲线
所对应的变换作用在曲线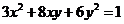 上,求所得曲线的方程.
上,求所得曲线的方程.
(2)选修4-4:坐标系与参数方程
已知在直角坐标系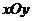 中,曲线
中,曲线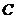 的参数方程为
的参数方程为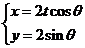 (t为非零常数,
(t为非零常数,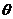 为参数),在极坐标系(与直角坐标系
为参数),在极坐标系(与直角坐标系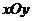 取相同的长度单位,且以原点
取相同的长度单位,且以原点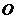 为极点,以
为极点,以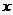 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线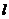 的方程为
的方程为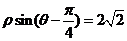 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数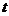 ,使得直线
,使得直线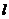 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点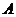 、
、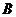 ,且
,且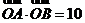 (其中
(其中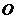 为坐标原点)?若存在,请求出;否则,请说明理由.
为坐标原点)?若存在,请求出;否则,请说明理由.
(3)选修4—5:不等式选讲
已知函数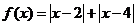 的最小值为
的最小值为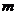 ,实数
,实数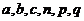 满足
满足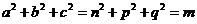 .
.
(Ⅰ)求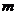 的值;
的值;
(Ⅱ)求证: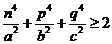 .
.
(1)选修:矩阵与变换
本题主要考查矩阵、逆矩阵、曲线的线性变换等基础知识,考查运算求解能力及函数与方程思想.满分7分.
解:(Ⅰ)记矩阵 ,故
,故 ,故
,故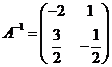 .
……2分
.
……2分
由已知得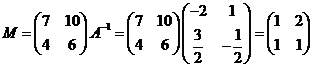 .
……3分
.
……3分
(Ⅱ)设二阶矩阵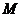 所对应的变换为
所对应的变换为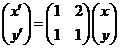 ,得
,得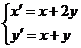 ,
,
解得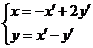 , ……5分
, ……5分
又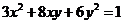 ,故有
,故有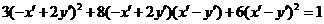 ,化简得
,化简得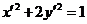 .故所得曲线的方程为
.故所得曲线的方程为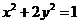 .
……7分
.
……7分
(2)选修:坐标系与参数方程
本题主要考查曲线的参数方程、直线的极坐标方程等基础知识,考查运算求解能力以及化归与转化思想、分类与整合思想.满分7分.
解:(Ⅰ)∵ ,∴可将曲线C的方程化为普通方程:
,∴可将曲线C的方程化为普通方程: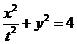 .
……1分
.
……1分
①当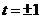 时,曲线C为圆心在原点,半径为2的圆;
……2分
时,曲线C为圆心在原点,半径为2的圆;
……2分
②当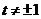 时,曲线C为中心在原点的椭圆. ……3分
时,曲线C为中心在原点的椭圆. ……3分
(Ⅱ)直线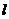 的普通方程为:
的普通方程为: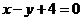 .
……4分
.
……4分
联立直线与曲线的方程,消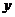 得
得 ,化简得
,化简得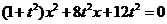 .
.
若直线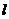 与曲线C有两个不同的公共点,则
与曲线C有两个不同的公共点,则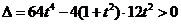 ,解得
,解得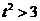 .
.
……5分
又 ……6分
……6分
故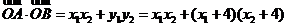
 .
.
解得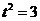 与
与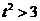 相矛盾.
相矛盾.
故不存在满足题意的实数 . ……7分
. ……7分
(3)选修;不等式选讲
本题主要考查绝对值的几何意义、柯西不等式等基础知识,考查运算求解能力以及推理论证能力,考查函数与方程思想以及分类与整合思想.满分7分.
解:(Ⅰ)法一: 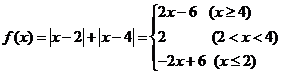 ,……2分
,……2分
可得函数的最小值为2.故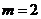 .
……3分
.
……3分
法二: , ……2分
, ……2分
当且仅当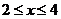 时,等号成立,故
时,等号成立,故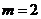 .
……3分
.
……3分
(Ⅱ)
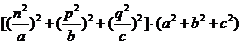
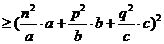 ……5分
……5分
即: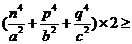
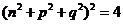 ,
,
故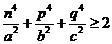 . ……7分
. ……7分
