题目内容
(理)已知f(x)=ax3+bx2+cx+d(a≠0)是定义在R上的函数,其图象交x轴于A、B、C三点.若点B的坐标为(2,0),且f(x)在［-1,0］和［4,5］上有相同的单调性,在［0,2］和［4,5］上有相反的单调性.(1)求c的值.
(2)在函数f(x)的图象上是否存在一点M(x0,y0),使得f(x)在点M处的切线斜率为3b?若存在,求出点M的坐标;若不存在,请说明理由.
(3)求|AC|的取值范围.
(文)已知函数f(x)=x4-4x3+ax2-1在区间［0,1］单调递增,在区间［1,2)单调递减.
(1)求a的值;
(2)若点A(x0,f(x0))在函数f(x)的图象上,求证点A关于直线x=1的对称点B也在函数f(x)的图象上;
(3)是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,若存在,请求出实数b的值;若不存在,试说明理由.
(理)解：(1)f′(x)=3ax2+2bx+c.
依题意f(x)在［-1,0］和［0,2］上有相反的单调性.
所以x=0是f(x)的一个极值点.
故f′(0)=0,得c=0.
(2)令f′(x)=0,得3ax2+2bx=0.
解得x1=0,x2=
.
因为f(x)在［0,2］和［4,5］上有相反的单调性,
所以f′(x)在［0,2］和［4,5］上有相反的符号.
故2≤
≤4
-6≤
≤-3.
假设存在点M(x0,y0)使得f(x)在点M处的切线斜率为3b,则f′(x0)=3b,
即3ax02+2bx0-3b=0.
因为Δ=(2b)2-4×3a(-3b)=4b2+36ab=4ab(
+9),
且-6≤
≤-3,所以3≤
+9≤6,且a、b异号.
所以Δ=4ab(
+9)＜0.
故不存在点M(x0,y0),使得f(x)在点M处的切线斜率为3b.
(3)设A(α,0),C(β,0),依题意可令f(x)=a(x-α)(x-2)(x-β),
即f(x)=a［x3-(2+α+β)x2+(2α+2β+αβ)x-2αβ］
=ax3-a(2+α+β)x2+a(2α+2β+αβ)x-2aαβ.
所以
即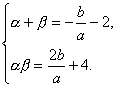
.
所以|AC|=|α-β|=
.
因为-6≤
≤-3,所以当
=-6时,|AC|max=
;
当
=-3时,|AC|min=3.
故3≤|AC|≤4
.
(文)解：(1)由函数f(x)=x4-4x3+ax2-1在区间［0,1］上单调递增,在区间［1,2)上单调递减,所以x=1时,取得极大值.
所以f′(1)=0.
因为f′(x)=4x3-12x2+2ax,
所以4-12+2a=0.解得a=4.
(2)因为点A(x0,f(x0))关于直线x=1的对称点B的坐标为(2-x0,f(x0)),
且f(2-x0)=(2-x0)4-4(2-x0)3+4(2-x0)2-1
=(2-x0)2［(2-x0)-2］2-1
=x04-4x03+4x02-1=f(x0).
所以点A关于直线x=1的对称点B也在函数f(x)的图象上.
(3)因为函数g(x)=bx2-1的图象与函数f(x)的图象恰有3个交点,
等价于方程x4-4x3+4x2-1=bx2-1恰有3个不等实根.
由x4-4x3+4x2-1=bx2-1,得x4-4x3+(4-b)x2=0.
因为x=0是其中一个根,
所以方程x2-4x+(4-b)=0有2个非零且不等的实数根.
故由
得b＞0且b≠4.
七星图书口算速算天天练系列答案
初中学业考试导与练系列答案
R)，l(x)= 2x2+3x-1，h (x)为f (x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求
；
，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；
), g(x)=cos(x－
(x∈R)在区间[-1，1]上是增函数。
的两个非零实根为x1、x2.试问：是否存在实数m，使得不等式m2+tm+1≥|x1-x2|对任意a∈A及t∈[-1，1]恒成立？若存在，求m的取值范围；若不存在，请说明理由。