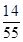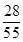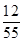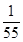题目内容
某单位为了提髙员工身体素质,特于近期举办了一场跳绳比赛,其中男员工12人,女员工18人,其成绩编成如右所示的茎叶图(单位:分).若分数在175分以上(含175分)者定为“运动健将”,并给以特别奖励,其它人员则给予“运动积极分子”称号,同时又特别提议给女“运动健将”休假一天的待遇.
(1)若用分层抽样的方法从“运动健将”和“运动积极分子”中提取10人,然后再从这10人中选4人,那么至少有1人是“运动健将”的概率是多少?
(2)若从所有“运动健将”中选3名代表,用 表示所选代表中女“运动健将”的人数,试写出
表示所选代表中女“运动健将”的人数,试写出 的分布列,并求
的分布列,并求 的数学期望.
的数学期望.

【答案】
(1)根据茎叶图,有“运动健将”12人,“运动积极分子”18人………1分
用分层抽样的方法,每个人被抽中的概率是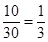 .
.
所以选中的“运动健将”有4人,“运动积极分子”有6人……………3分
用事件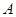 表示“至少有一名‘运动健将’被选中”
表示“至少有一名‘运动健将’被选中”
则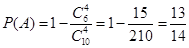 …………………………………5分
…………………………………5分
因此,至少有一人是“运动健将”的概率是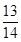 ………………………6分
………………………6分
(2)依题意,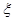 的取值为0,1,2,3………………………7分
的取值为0,1,2,3………………………7分
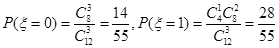
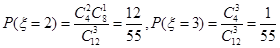 ……………………9分
……………………9分
因此,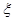 的分布列如下
的分布列如下
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
…………………………………………………………………………………10分
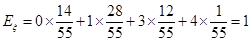 ……………………………………12分
……………………………………12分
【解析】略

练习册系列答案
相关题目