题目内容
.已知定义在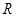 上的奇函数
上的奇函数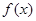 和偶函数
和偶函数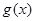 满足
满足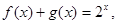 若不等式
若不等式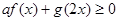 对
对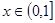 恒成立,则实数
恒成立,则实数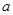 的取值范围是________。
的取值范围是________。
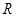 上的奇函数
上的奇函数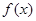 和偶函数
和偶函数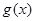 满足
满足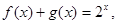 若不等式
若不等式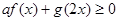 对
对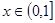 恒成立,则实数
恒成立,则实数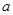 的取值范围是________。
的取值范围是________。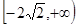
分析:先根据函数奇偶性定义,解出奇函数f(x)和偶函数g(x)的表达式,将这个表达式不等式af(x)+g(2x)≥0,通过变形可得a≥-
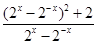 ,再通过换元,讨论出右边在x∈(0,1]的最大值,可以得出实数a的取值范围.
,再通过换元,讨论出右边在x∈(0,1]的最大值,可以得出实数a的取值范围.解:∵f(x)为定义在R上的奇函数,g(x)为定义在R上的偶函数
∴f(-x)=-f(x),g(-x)=g(x)
又∵由f(x)+g(x)=2x,结合f(-x)+g(-x)=-f(x)+g(x)=2-x,
∴f(x)=
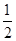 (2x-2-x),g(x)=
(2x-2-x),g(x)=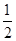 (2x+2-x)
(2x+2-x)不等式af(x)+g(2x)≥0,化简为
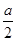 (2x-2 -x) +
(2x-2 -x) +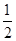 (2 2x+2-2x) ≥0
(2 2x+2-2x) ≥0∵0<x<1
∴0<2x<2-2-x<1
因此将上面不等式整理,得:a≥-
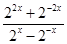 =-
=-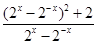
令t=2x-2-x,则t>0
∴-
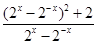 =-(t+
=-(t+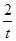 )≤ -2
)≤ -2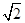
因此,实数a的取值范围是a≥- 2
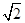
故答案为[-2
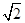 ,+∞)
,+∞)
练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
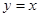
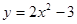
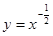
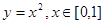
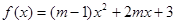 为偶函数,则
为偶函数,则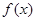 在(—5,—2)上是( )
在(—5,—2)上是( )
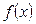 满足:对任意的
满足:对任意的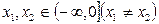 ,有
,有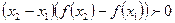 .则当
.则当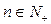 时,有
时,有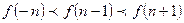
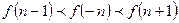
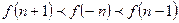
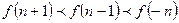
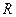 的函数
的函数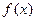 为偶函数,且当
为偶函数,且当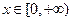 时,
时,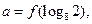
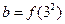 ,
,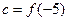 ,则
,则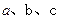 的大小关系是( )
的大小关系是( )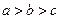
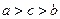
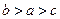
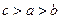
 为偶函数,且当
为偶函数,且当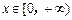 时,
时,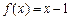 ,则不等式
,则不等式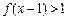 的解集为
的解集为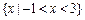
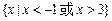
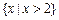
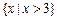
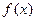 在R上为奇函数,且
在R上为奇函数,且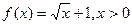 ,则当
,则当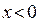 ,
,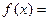
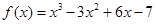 的图象是中心对称图形,其对称中心为
的图象是中心对称图形,其对称中心为