题目内容
已知椭圆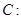
 的左焦点为
的左焦点为 ,左、右顶点分别为
,左、右顶点分别为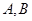 ,过点
,过点 且倾斜角为
且倾斜角为 的直线
的直线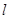 交椭圆于
交椭圆于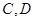 两点,椭圆
两点,椭圆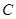 的离心率为
的离心率为 ,
, .
.
(1)求椭圆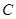 的方程;
的方程;
(2)若 是椭圆上不同两点,
是椭圆上不同两点,
 轴,圆
轴,圆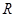 过点
过点 ,且椭圆上任意一点都不在圆
,且椭圆上任意一点都不在圆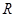 内,则称圆
内,则称圆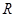 为该椭圆的内切圆.问椭圆
为该椭圆的内切圆.问椭圆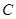 是否存在过点
是否存在过点 的内切圆?若存在,求出点
的内切圆?若存在,求出点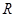 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(1)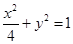 ;(2)存在
;(2)存在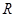
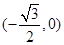
解析试题分析:(1)由离心率为 ,倾斜角为
,倾斜角为 的直线
的直线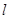 交椭圆于
交椭圆于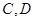 两点,
两点,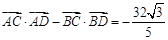 .通过联立直线方程与椭圆的方程,可求得
.通过联立直线方程与椭圆的方程,可求得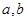 的值.即可得结论.
的值.即可得结论.
(2)依题意可得符合要求的圆E,即为过点 ,
,  的三角形的外接圆.所以圆心在x轴上.根据题意写出圆E的方程.由于圆的存在必须要符合,椭圆上的点到点
的三角形的外接圆.所以圆心在x轴上.根据题意写出圆E的方程.由于圆的存在必须要符合,椭圆上的点到点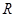 距离的最小值是
距离的最小值是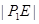 ,结合图形可得圆心
,结合图形可得圆心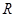 在线段
在线段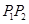 上,半径最小.又由于点F已知,即可求得结论.
上,半径最小.又由于点F已知,即可求得结论.
试题解析:(1)因为离心率为 ,所以
,所以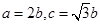 ,
,
所以椭圆方程可化为: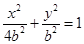 ,直线
,直线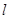 的方程为
的方程为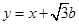 , 2分
, 2分
由方程组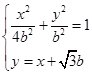 ,得:
,得: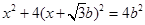 ,即
,即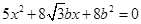 , 4分
, 4分
设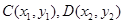 ,则
,则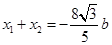 , 5分
, 5分
又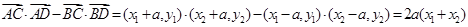 ,
,
所以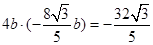 ,所以
,所以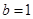 ,椭圆方程是
,椭圆方程是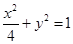 ; 7分
; 7分
(2)由椭圆的对称性,可以设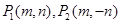 ,点
,点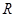 在
在 轴上,设点
轴上,设点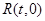 ,
,
则圆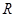 的方程为
的方程为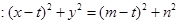 ,
,
由内切圆定义知道,椭圆上的点到点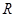 距离的最小值是
距离的最小值是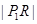 ,
,
设点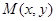 是椭圆
是椭圆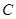 上任意一点,则
上任意一点,则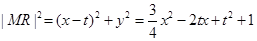 , 9分
, 9分
当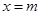 时,
时,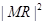 最小,所以
最小,所以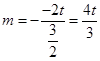 ① 10分
① 10分
又圆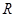 过点
过点 ,所以
,所以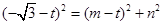 ② 11分
② 11分
点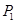 在椭圆上,所以
在椭圆上,所以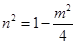 ③ 12分
③ 12分
由①②③解得: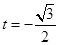 或
或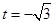 ,
,
又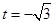 时,
时,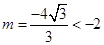 ,不合,
,不合,
综上:椭圆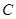 存在符合条件的内切圆,点
存在符合条件的内切圆,点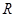 的坐标是
的坐标是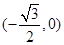 . 13分
. 13分
考点:1.待定系数求椭圆方程.2.函数的最值.3.方程的思想解决解决解几问题.3.归纳化归的思想.4.运算能力.

练习册系列答案
相关题目
 a为常数且a>0.
a为常数且a>0. 对称;
对称;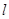 (宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数
(宽度不计),切点为M,并把该地块分为两部分.现以点O为坐标原点,以线段OC所在直线为x轴,建立平面直角坐标系,若池边AE满足函数 )的图象,且点M到边OA距离为
)的图象,且点M到边OA距离为 .
.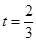 时,求直路
时,求直路
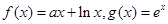 .
.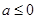 时,求
时,求 的单调区间;
的单调区间;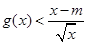 有解,求实数m的取值菹围;
有解,求实数m的取值菹围;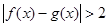 .
.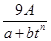 ,其中
,其中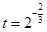 ,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍.
,a,b为常数,n∈N,f(0)=A.已知栽种3年后该树木的高度为栽种时高度的3倍. 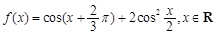 .
. 的值域;
的值域;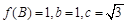 ,求a的值.
,求a的值. 的定义域为E,值域为F.
的定义域为E,值域为F.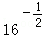 与集合F的关系;
与集合F的关系;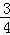 },求实数a的值.
},求实数a的值.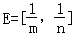 ,F=[2﹣3m,2﹣3n],求m,n的值.
,F=[2﹣3m,2﹣3n],求m,n的值.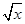 +2)=x+4
+2)=x+4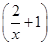 =lgx,求f(x);
=lgx,求f(x);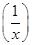 =2x,x∈R且x≠0,求f(x);
=2x,x∈R且x≠0,求f(x);