题目内容
实数a、b满足a＞b＞0，集合
，
，则集合
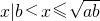可表示为
- A.M∪N
- B.M∩N
- C.CRM∩N
- D.M∩CRN
D
分析：先利用均值不等式，得
，再利用集合的补集的定义求出CRN，利用两个集合的交集的定义求出 M∩CRN即可得到答案．
解答：∵实数a、b满足a＞b＞0，
∴，
∵全集U=R，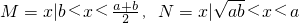
，
∴CRN={x|x≤
，或 x≥a }，
M∩CRN=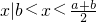
∩{x|x≤，或 x≥a }
=，
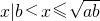故选D．
点评：本题考查基本不等式、集合的表示方法、集合的补集，两个集合的交集的定义和求法，求出CRN={x|x≤，或 x≥a }，是解题的关键．
分析：先利用均值不等式，得
，再利用集合的补集的定义求出CRN，利用两个集合的交集的定义求出 M∩CRN即可得到答案．解答：∵实数a、b满足a＞b＞0，
∴
，∵全集U=R，
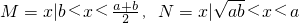，∴CRN={x|x≤
，或 x≥a }，M∩CRN=
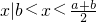∩{x|x≤，或 x≥a }=
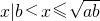，故选D．
点评：本题考查基本不等式、集合的表示方法、集合的补集，两个集合的交集的定义和求法，求出CRN={x|x≤
，或 x≥a }，是解题的关键． 
练习册系列答案
相关题目
设非零实数a，b满足a＜b，则下列不等式中一定成立的是（ ）
A、
| ||||
| B、ab＜b2 | ||||
| C、a+b＞0 | ||||
| D、a＜|b| |
﹣a﹣b那么φ(a，b）=0是a与b互补的