题目内容
投资生产某种产品,并用广告方式促销,已知生产这种产品的年固定投资为10万元,每生产1万件产品还需投入16万元,又知年销量W(万件)与广告费x(万元)之间的函数关系为W=k-
(x>0),且已知投入广告费1万元时,年销量为2万件产品.预计此种产品年销售收入M(万元)等于年成本(万元)(年成本中不含广告费用)的150%与年广告费用(万元)的50%的和.
(1)试将年利润y(万元)表示为年广告费x(万元)的函数;
(2)当年广告费为多少万元时,年利润最大?最大年利润是多少万元?
| 1 | x |
(1)试将年利润y(万元)表示为年广告费x(万元)的函数;
(2)当年广告费为多少万元时,年利润最大?最大年利润是多少万元?
分析:(1)由已知中年销量W(万件)与广告费x(万元)之间的函数关系为W=k-
(x>0),投入广告费1万元时,年销量为2万件产品,代入可以求出k值,进而得到W的表达式,进而求出结合年销售收入,结合年成本为10+16w+x,根据利润=收入-成本,即可得到年利润y(万元)表示为年广告费x(万元)的函数;
(2)根据(1)中得到的函数解析式,根据基本不等式,易得到年广告费为多少万元时,年利润最大及对应的最大年利润是多少万元.
| 1 |
| x |
(2)根据(1)中得到的函数解析式,根据基本不等式,易得到年广告费为多少万元时,年利润最大及对应的最大年利润是多少万元.
解答:解:(1)∵W=k-
(x>0),且投入广告费1万元时,年销量为2万件产品∴k=3,∴W=3-
…(2分)
年销售收入M=
(10+16w)+
x,年成本为10+16w+x
…(4分)
∴y=
[58-(
+x)] …(8分)
(2)y=
[58-(
+x)]≤
(58-2
)=25,…(12分)
当且仅当
=x,即x=4时,等号成立…(14分)
所以当x=4时,ymax=25 …(15分)
答:当年广告费为4万元时,年利润最大,最大年利润是25万元.…(16分)
| 1 |
| x |
| 1 |
| x |
年销售收入M=
| 3 |
| 2 |
| 1 |
| 2 |
|
∴y=
| 1 |
| 2 |
| 16 |
| x |
(2)y=
| 1 |
| 2 |
| 16 |
| x |
| 1 |
| 2 |
|
当且仅当
| 16 |
| x |
所以当x=4时,ymax=25 …(15分)
答:当年广告费为4万元时,年利润最大,最大年利润是25万元.…(16分)
点评:本题考查的知识点是函数模型的选择与应用,其中根据已知条件分别计算年销售收入的表达式工,及年成本的表达式,进而根据利润=收入-成本,得到年利润的表达式是解答本题的关键.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
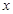 (
( )件.当
)件.当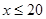 时,年销售总收入为(
时,年销售总收入为(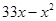 )万元;当
)万元;当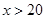 时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为
时,年销售总收入为260万元.记该工厂生产并销售这种产品所得的年利润为 万元,则
万元,则 年总投资)
年总投资)