题目内容
已知函数 满足
满足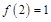 ,且
,且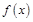 的导函数
的导函数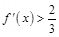 ,则关于
,则关于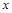 的不等式
的不等式 的解集为 .
的解集为 .
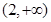 .
.
解析试题分析:因为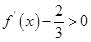 ,∴
,∴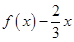 在R上是单调递增的函数;而
在R上是单调递增的函数;而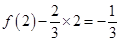 ,即
,即 所以不等式的解集为
所以不等式的解集为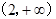 .
.
考点:导函数的应用、不等式的解法.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
题目内容
已知函数 满足
满足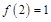 ,且
,且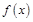 的导函数
的导函数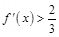 ,则关于
,则关于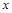 的不等式
的不等式 的解集为 .
的解集为 .
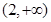 .
.
解析试题分析:因为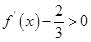 ,∴
,∴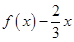 在R上是单调递增的函数;而
在R上是单调递增的函数;而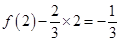 ,即
,即 所以不等式的解集为
所以不等式的解集为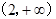 .
.
考点:导函数的应用、不等式的解法.

 一本好题口算题卡系列答案
一本好题口算题卡系列答案