题目内容
(本题满分12分)某商场预计2009年1月份起前x个月,顾客对某种商品的需求总量p(x)(单位:件)与x的关系近似地满足p(x)=![]() x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
x(x+1)(39-2x),(x∈N*,且x≤12).该商品第x月的进货单价q(x)(单位:元)与x的近似关系是q(x)=150+2x.(x∈N*,且x≤12).(1)写出今年第x月的需求量f(x)件与x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问商场2009年第几月份销售该商品的月利润最大,最大月利润为多少元?
(Ⅰ) f(x)=-3x2+40x(x∈N*,且1≤x≤12). (Ⅱ) 最大利润为3125元
解析:
(1)当x=1时,f(1)=p(1)=37,当2≤x≤12时,f(x)=p(x)-p(x-1)=![]() x(x+1)(39-2x)---
x(x+1)(39-2x)---![]() (x-1)x(41-2x) =-3x2+40x (x∈N*,且2≤x≤12). 验证x=1符合f(x)=-3x2+40x(x∈N*,且1≤x≤12). --------6分
(x-1)x(41-2x) =-3x2+40x (x∈N*,且2≤x≤12). 验证x=1符合f(x)=-3x2+40x(x∈N*,且1≤x≤12). --------6分
(2)该商场预计第x月销售该商品的月利润为
g(x)=(-3x2+40x)(185-150-2x)=6x3-185x2+1400x(x∈N*,且1≤x≤12).
|
当1≤x<5时,g′(x) >0,当5<x≤12时,g′(x) <0,∴当x=5时,g(x)max=g(5)=3125(元).
综上,商场2009年第5月份的月利润最大,最大利润为3125元.-------12分

练习册系列答案
相关题目
 ,
, ,…,
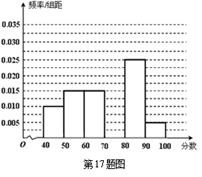
,…,  后得到如下频率分布直方图.
后得到如下频率分布直方图.
 内的频率;
内的频率; 两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套
两型会议桌,每套会议桌需经过加工木材和上油漆两道工序才能完成。已知做一套 的厂房(不管墙高),工程的造价是:
的厂房(不管墙高),工程的造价是: