题目内容
有下列四个命题:
①函数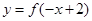 与
与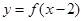 的图象关于
的图象关于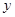 轴对称;②若函数
轴对称;②若函数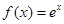 ,则对
,则对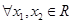 ,都有
,都有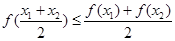 ;③若函数
;③若函数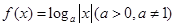 在区间
在区间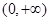 上单调递增,则
上单调递增,则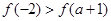 ;
④若函数
;
④若函数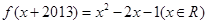 ,则函数
,则函数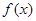 的最小值为
的最小值为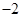 .其中真命题的序号是
.
.其中真命题的序号是
.
【答案】
②④
【解析】
试题分析:①函数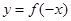 与
与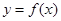 的图象关于
的图象关于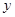 轴对称,将函数
轴对称,将函数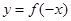 与
与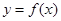 的图象都向右平移2个单位,便得函数
的图象都向右平移2个单位,便得函数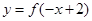 与
与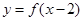 的图象,所以函数
的图象,所以函数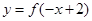 与
与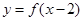 的图象关于
的图象关于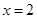 对称;②作出函数
对称;②作出函数 的图象,从图象可看出结论成立(函数的凸性).
的图象,从图象可看出结论成立(函数的凸性).
③函数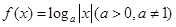 在区间
在区间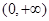 上单调递增,所以
上单调递增,所以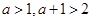 从而
从而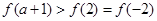 ;④将函数图象左右平移,函数的最大值最小值不变,所以函数
;④将函数图象左右平移,函数的最大值最小值不变,所以函数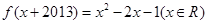 与函数
与函数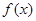 的最小值相同.
的最小值相同.
考点:本题综合考查函数的图象及性质.

练习册系列答案
相关题目