题目内容
函数y=ax2+bx与y=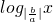
（ab≠0，|a|≠|b|）在同一直角坐标系中的图象可能是
- A.
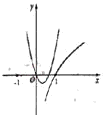
- B.
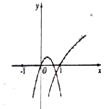
- C.
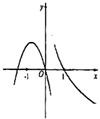
- D.
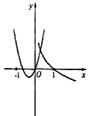
D
分析：可采用反证法做题，假设A和B的对数函数图象正确，由二次函数的图象推出矛盾，所以得到A和B错误；同理假设C和D的对数函数图象正确，根据二次函数图象推出矛盾，得到C错误，D正确．
解答：对于A、B两图，|
|＞1而ax2+bx=0的两根为0和-，且两根之和为-，由图知0＜-＜1得-1＜＜0，矛盾，
对于C、D两图，0＜||＜1，在C图中两根之和-＜-1，即＞1矛盾，C错，D正确．
故选D．
点评：考查学生会利用反证法的思想解决实际问题，要求学生掌握二次函数和对数函数的图象和性质．
分析：可采用反证法做题，假设A和B的对数函数图象正确，由二次函数的图象推出矛盾，所以得到A和B错误；同理假设C和D的对数函数图象正确，根据二次函数图象推出矛盾，得到C错误，D正确．
解答：对于A、B两图，|
|＞1而ax2+bx=0的两根为0和-，且两根之和为-，由图知0＜-＜1得-1＜＜0，矛盾，对于C、D两图，0＜|
|＜1，在C图中两根之和-＜-1，即＞1矛盾，C错，D正确．故选D．
点评：考查学生会利用反证法的思想解决实际问题，要求学生掌握二次函数和对数函数的图象和性质．
练习册系列答案
相关题目
如图已知O为坐标原点，∠AOB=30°，∠ABO=90°，且点A的坐标为（2，0）．
如图，已知二次函数y=x2-2x-1的图象的顶点为A．二次函数y=ax2+bx的图象与x轴交于原点O及另一点C，它的顶点B在函数y=x2-2x-1的图象的对称轴上．