题目内容
已知圆C满足以下条件:(1)圆上一点A关于直线x+2y=0的对称点B仍在圆上,(2)圆心在直线3x-2y-8=0上,(3)与直线x-y+1=0相交截得的弦长为2| 2 |
分析:先假设圆的方程为(x-a)2+(y-b)2=r2(r>0),由(1)知圆心在直线上;由(2)知3a-2b-8=0,再利用(3)求圆的半径,故问题得解.
解答:解:设圆的方程为(x-a)2+(y-b)2=r2(r>0),∵圆上一点A关于直线x+2y=0的对称点B仍在圆上,∴a+2b=0
∵圆心在直线3x-2y-8=0上,∴3a-2b-8=0,∴a=2,b=-1
∵与直线x-y+1=0相交截得的弦长为2
,∴
2+2=r2,∴r2=10,∴(x-2)2+(y+1)2=10
∵圆心在直线3x-2y-8=0上,∴3a-2b-8=0,∴a=2,b=-1
∵与直线x-y+1=0相交截得的弦长为2
| 2 |
| (a-b+1) |
| 2 |
点评:本题考查圆的方程,解题时要用到直线的距离公式和勾股定理的合理运用.结合图形进行求解会收到良好的效果.

练习册系列答案
相关题目
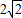 ,求圆C的方程.
,求圆C的方程.