题目内容
已知圆C满足以下三个条件:①圆心在直线x-y-1=0上,②与直线4x+3y+14=0相切,③截直线3x+4y+10=0所得弦长为6.求圆C的方程.
分析:根据题意设圆心坐标为(a,a-1),根据圆与直线4x+3y+14=0的距离d等于圆的半径r,表示出r,根据圆与直线3x+4y+10=0截得的弦长为6,列出关于a的方程,求出方程的解得到a的值,确定出圆心坐标与半径,写出圆的方程即可.
解答:解:设圆心坐标为(a,a-1),
∵圆与直线4x+3y+14=0相切,
∴圆心到切线的距离d=
=r,
∵圆截直线3x+4y+10=0所得弦长为6,圆心到直线3x+4y+10=0的距离为
,
∴2
=6,
解得:a=2,
∴圆心坐标为(2,1),半径r=5,
则圆方程为(x-2)2+(y-1)2=25.
∵圆与直线4x+3y+14=0相切,
∴圆心到切线的距离d=
| |7a+11| |
| 5 |
∵圆截直线3x+4y+10=0所得弦长为6,圆心到直线3x+4y+10=0的距离为
| |7a+6| |
| 5 |
∴2
(
|
解得:a=2,
∴圆心坐标为(2,1),半径r=5,
则圆方程为(x-2)2+(y-1)2=25.
点评:此题考查了直线与圆的位置关系,涉及的知识有:点到直线的距离公式,垂径定理,勾股定理,以及圆的标准方程,熟练掌握定理及公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
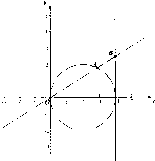 已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足
已知点A(x1,y1)在圆(x-2)2+y2=4上运动,点A不与(0,0)重合,点B(4,y0)在直线x=4上运动,动点M(x,y)满足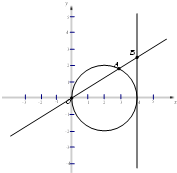 (2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足
(2011•南汇区二模)已知动直线y=kx交圆(x-2)2+y2=4于坐标原点O和点A,交直线x=4于点B,若动点M满足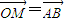 ,动点M的轨迹C的方程为F(x,y)=0.
,动点M的轨迹C的方程为F(x,y)=0.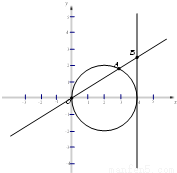
 .动点M的轨迹C的方程为F(x,y)=0.
.动点M的轨迹C的方程为F(x,y)=0.