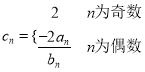题目内容
【题目】已知![]() 是定义在
是定义在![]() 上的奇函数,且
上的奇函数,且![]() .若对任意的
.若对任意的![]() ,
, ![]() 都有
都有![]() .
.
(1)用函数单调性的定义证明: ![]() 在定义域上为增函数;
在定义域上为增函数;
(2)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)若不等式![]() 对所有的
对所有的![]() 和
和![]() 都恒成立,求实数
都恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】试题分析:(1)任取![]() ,作差
,作差![]() ,可证明
,可证明![]() 从而可得结果;(2)根据函数的单调性,结合函数的定义域,列出关于
从而可得结果;(2)根据函数的单调性,结合函数的定义域,列出关于![]() 的不等式组,解不等式组即可得结果;(3)不等式
的不等式组,解不等式组即可得结果;(3)不等式![]() 恒成立等价于
恒成立等价于![]() ,即
,即![]() 对任意
对任意![]() 恒成立,根据一次函数的性质可得结果.
恒成立,根据一次函数的性质可得结果.
试题解析:(1)设![]() ,
, ![]() ,
,
![]()
![]() ,∴
,∴![]() 在
在![]() 上为增函数.
上为增函数.
(2)![]()
![]() 在
在![]() 单调递增,
单调递增,
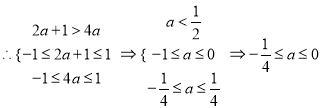 .
.
(3)要使![]() 对任意
对任意![]() 恒成立,只要
恒成立,只要![]() 在
在![]() 即可,由(1)知
即可,由(1)知![]() 在
在![]() 单调递增,
单调递增, ![]() ,
, ![]() ,
, ![]() 对任意
对任意![]() 恒成立,令
恒成立,令![]() ,只要
,只要![]() 且
且![]() 即可,
即可, ![]() 且
且![]() .
.
【方法点晴】本题主要考查抽象函数的定义域、抽象函数的单调性及抽象函数解不等式,属于难题.根据抽象函数的单调性解不等式应注意以下三点:(1)一定注意抽象函数的定义域(这一点是同学们容易疏忽的地方,不能掉以轻心);(2)注意应用函数的奇偶性(往往需要先证明是奇函数还是偶函数);(3)化成![]() 后再利用单调性和定义域列不等式组.
后再利用单调性和定义域列不等式组.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某公司有![]() 五辆汽车,其中
五辆汽车,其中![]() 两辆汽车的车牌尾号均为1.
两辆汽车的车牌尾号均为1. ![]() 两辆汽车的车牌尾号均为2,
两辆汽车的车牌尾号均为2, ![]() 车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车,
车的车牌尾号为6,已知在非限行日,每辆车可能出车或不出车, ![]() 三辆汽车每天出车的概率均为
三辆汽车每天出车的概率均为![]() ,
, ![]() 两辆汽车每天出车的概率均为
两辆汽车每天出车的概率均为![]() ,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
,且五辆汽车是否出车相互独立,该公司所在地区汽车限行规定如下:
车牌尾号 | 0和5 | 1和6 | 2和7 | 3和8 | 4和9 |
限行日 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 |
(1)求该公司在星期一至少有2辆汽车出国的概率;
(2)设![]() 表示该公司在星期二和星期三两天出车的车辆数之和,求
表示该公司在星期二和星期三两天出车的车辆数之和,求![]() 的分布列及期望.
的分布列及期望.