题目内容
已知向量![]() ,动点
,动点![]() 到定直线
到定直线![]() 的距离等于
的距离等于![]() ,并且满足
,并且满足![]() ,其中
,其中![]() 为坐标原点,
为坐标原点,![]() 为非负实数.
为非负实数.
(1)求动点![]() 的轨迹方程
的轨迹方程![]() ;
;
(2)若将曲线![]() 向左平移一个单位,得曲线
向左平移一个单位,得曲线![]() ,试判断曲线
,试判断曲线![]() 为何种类型;
为何种类型;
(3)若(2)中曲线![]() 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足![]() ,当
,当![]() 是曲线
是曲线![]() 的两个焦点时,则圆锥曲线上恒存在点
的两个焦点时,则圆锥曲线上恒存在点![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
(1)![]() (2)见解析(3)
(2)见解析(3)![]()
解析:
(1)设动点![]() ,则由
,则由![]() ,
,![]() 为坐标原点,得
为坐标原点,得![]()
![]()
![]()
![]() 由
由![]() ,得
,得![]() 为所求的动点
为所求的动点![]() 的轨迹方程;
的轨迹方程;
(2)将曲线![]() 向左平移一个单位,得曲线
向左平移一个单位,得曲线![]() 的方程为
的方程为![]() (
(![]() )
)
①当![]() 时,得
时,得![]() ,曲线
,曲线![]() 为一条直线;
为一条直线;
②当![]() 时,得
时,得![]() .若
.若![]() ,曲线
,曲线![]() 为圆;若
为圆;若![]() ,曲线
,曲线![]() 为双曲线;若
为双曲线;若![]() ,曲线
,曲线![]() 为焦点在
为焦点在![]() 轴上的椭圆;
轴上的椭圆;
(3)若(2)中曲线![]() 为圆锥曲线,其离心率满足
为圆锥曲线,其离心率满足![]() ,则曲线
,则曲线![]() 为焦点在
为焦点在![]() 轴上的椭圆,
轴上的椭圆,
![]() 圆锥曲线上恒存在点
圆锥曲线上恒存在点![]() ,使得
,使得![]() 成立,
成立,![]()
![]()
即以![]() 为直径的圆与椭圆恒有交点.
为直径的圆与椭圆恒有交点. ![]()
![]()
综上得实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 动点
动点 到定直线
到定直线 的距离等于
的距离等于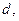 并且满足
并且满足 其中O是坐标原点,
其中O是坐标原点, 是参数.
是参数. 时,求
时,求 的最大值和最小值;
的最大值和最小值; 满足
满足 求实数
求实数 动点
动点 到定直线
到定直线 的距离等于
的距离等于 并且满足
并且满足 其中
其中 是坐标原点,
是坐标原点, 是参数.
是参数. 时,求
时,求 的最大值和最小值;
的最大值和最小值; 满足
满足 求实数
求实数