题目内容
已知函数 在
在 与
与 时都取得极值
时都取得极值
(1)求 的值与函数
的值与函数 的单调区间
的单调区间
(2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。
【答案】
(1)函数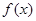 的递增区间是
的递增区间是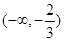 与
与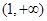 ,递减区间是
,递减区间是 ;
;
(2)
【解析】
试题分析:解:(1)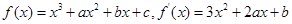
由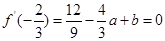 ,
,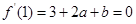 得
得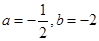
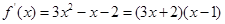 ,函数
,函数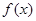 的单调区间如表:
的单调区间如表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
极大值 |
¯ |
极小值 |
|
所以函数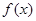 的递增区间是
的递增区间是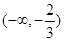 与
与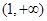 ,递减区间是
,递减区间是 ;
;
(2)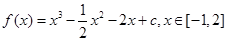 ,当
,当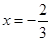 时,
时,
为极大值,而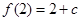 ,则
,则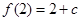 为最大值,要使
为最大值,要使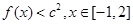
恒成立,则只需要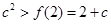 ,得
,得 。
。
考点:导数的运用
点评:主要是考查了导数的运用来求解单调性和最值的运用,属于基础题。

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
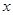

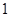
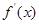
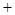

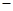
 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值
时都取得极值 的值 (2)若对
的值 (2)若对 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围
的取值范围  在
在 与
与 时都取得极值。
时都取得极值。 的值及函数
的值及函数 的单调区间;
的单调区间; 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值
时都取得极值 的值与函数
的值与函数 的单调区间
的单调区间 ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围。
的取值范围。 在
在 与
与 时都取得极值.
时都取得极值. 的值及函数
的值及函数 的单调区间;
的单调区间; ,不等式
,不等式 恒成立,求
恒成立,求 的取值范围.
的取值范围.