题目内容
已知函数 (k∈R),若函数
(k∈R),若函数 有三个零点,则实数k的取值范围是( )
有三个零点,则实数k的取值范围是( )
| A.k≤2 | B.-1<k<0 |
| C.-2≤k<-1 | D.k≤-2 |
D
解析试题分析:由 =0得|f(x)|=-k≥0,
=0得|f(x)|=-k≥0,
所以k≤0,作出函数y=|f(x)|的图象,
由图象可知:要使y=-k与函数y=|f(x)|有三个交点,
则有-k≥2,即k≤-2,
故选D。
考点:函数零点,分段函数的概念,一次函数、对数函数的图象和性质。
点评:中档题,首先将函数零点问题,转化成研究函数图象的交点问题,利用数形结合思想,结合函数图象,得到k的范围。

练习册系列答案
相关题目
已知f(x)的定义域是(0,1),则f[( )x]的定义域为( )
)x]的定义域为( )
| A.(0,1) | B.( ,1) ,1) | C.(-∞,0) | D.(0,+ ∞) |
设 ,则函数
,则函数 ( )
( )
A.在 上单调递减,在 上单调递减,在 上单调递增 上单调递增 |
B.在 上单调递增,在 上单调递增,在 上单调递减 上单调递减 |
C.在 上单调递增,在 上单调递增,在 上单调递增 上单调递增 |
D.在 上单调递减,在 上单调递减,在 上单调递减 上单调递减 |
函数 由
由 确定,则方程
确定,则方程 的实数解有( )
的实数解有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
若 ,则下列不等式成立的是( )
,则下列不等式成立的是( )
A. | B. | C. | D. |
函数y= ln(1-x)的定义域为( )
ln(1-x)的定义域为( )
| A.(0,1) | B.[0,1) | C.(0,1] | D.[0,1) |
设函数 为奇函数,
为奇函数, 则
则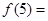 ( )
( )
| A.0 | B.1 | C. | D.5 |
三个数 的大小顺序是
的大小顺序是
| A.0.76<log0.76<60.7 | B.0.76<60.7<log0.76 |
| C.log0.76<60.7<0.76 | D. |
设 ,则这四个数的大小关系是( )
,则这四个数的大小关系是( )
A. | B. |
C. | D.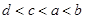 |