题目内容
15．已知f（x）=x3-$\frac{1}{2}$x2+bx+c的图象存在与直线y=1平行的切线，则b的取值范围是（-∞，$\frac{1}{12}$]．分析 求出函数f（x）的导数，由题意可得f′（x）=0有实数解，运用二次方程的判别式不小于0，即可解得b的范围．
解答 解：f（x）=x3-$\frac{1}{2}$x2+bx+c的导数为f′（x）=3x2-x+b，
由f（x）的图象存在与直线y=1平行的切线，
即有f′（x）=0有实数解，
则判别式△≥0，
即1-12b≥0，解得b≤$\frac{1}{12}$，
故答案为：（-∞，$\frac{1}{12}$]．
点评 本题考查导数的运用：求切线的斜率，主要考查导数的几何意义，注意运用二次方程有解是条件是解题的关键．
练习册系列答案
相关题目
6．数列3，15，35，63，（ ），143，…括号中的数字应为（ ）
| A． | 56 | B． | 72 | C． | 90 | D． | 99 |
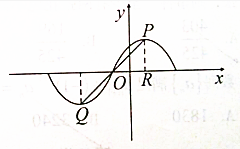已知函数f（x）=Acos（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜$\frac{π}{2}$），部分图象如图所示，PQ分别为图象的最高点和最低点，PR⊥x轴于R（$\frac{1}{2}$，0）点，∠RPQ=45°，|PQ|=2$\sqrt{2}$．