题目内容
下图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，中间的数字表示得分的十位数，下列对乙运动员的判断错误的是（ ）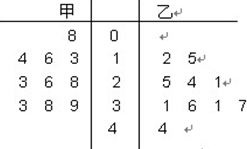 
| A．乙运动员得分的中位数是28 | B．乙运动员得分的众数为31 |
| C．乙运动员的场均得分高于甲运动员 | D．乙运动员的最低得分为0分 |
D
解析试题分析：从茎叶图中分析：乙运动员得分的中位数是28 ；乙运动员得分的众数为31；乙运动员的平均分为27.5，,甲运动员的平均分为23.6，因此乙运动员的场均得分高于甲运动员；乙运动员的最低得分为12分.因此选D .
考点：茎叶图；中位数；众数；平均值。
点评：本题主要考查茎叶图和中位数，是一个基础题，这种题目可以从茎叶图中直接看出中位数，而不用把这组数据写下来，但是若茎叶图中所给的数字没有按照大小顺序时，容易弄错。
练习册系列答案
口算题卡加应用题集训系列答案
相关题目
实验测得四组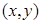
的值分别为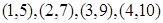
，则y关于x的线性回归方程必过点（ ）
| A．（2，8） | B．（2.5，8） |
| C．（10，31） | D．（2.5，7.75） |
一组数据中，每一个数都减去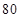
，得到一组新数据，若求得新数据的平均数是
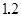，方差是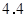
，则原来数据的平均数和方差分别为（ ）
A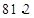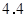． , | B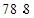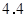． , | C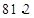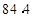．,  | D．, |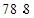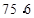
某商场在国庆黄金周的促销活动中，对10月2日9时至14时的销售额进行统计，其频率分布直方图如图1所示，已知9时至10时的销售额为2.5万元，则11时至12时的销售额为（ ）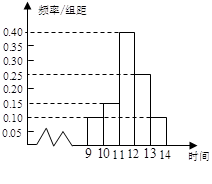
| A．6万元 | B．8万元 | C．10万元 | D．12万元 |
某比赛中，七位评委为某个节目打出的分数如右图茎叶统计图所示，去掉一个最高分和一个最低分后所剩数据的平均数和方差分别是（ ）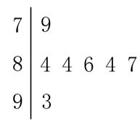 
| A．84, 4.84 | B．84， 16 | C．85， 1.6 | D．85， 4 |
某个小区住户共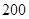
户,为调查小区居民的
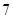月份用水量,用分层抽样的方法抽取了
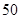户进行调查,得到本月的用水量(单位:m3)的频率分布直方图如图所示,则小区内用水量超过
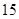m3的住户的户数为( )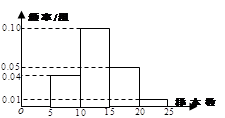
A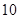． | B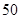． | C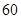． | D． |
某地区教育主管部门为了对该地区模拟考试成绩进行分析，抽取了总成绩介于350分到650分之间的10000名学生成绩，并根据这10000名学生的总成绩画了样本的频率分布直方图（如右图），则总成绩在［400，500）内共有（ ）
| A．5000 人 | B．4500人 |
| C．3250人 | D．2500人 |
有关线性回归的说法，不正确的是（ ）
| A．相关关系的两个变量不是因果关系 |
| B．散点图能直观地反映数据的相关程度 |
| C．回归直线最能代表线性相关的两个变量之间的关系 |
| D．任一组数据都有回归方程 |