题目内容
下列关于数列的命题①若数列{an}是等差数列,且p+q=r(p,q,r为正整数)则ap+aq=ar
②若数列{an}满足an+1=2an,则{an}是公比为2的等比数列
③2和8的等比中项为±4
④已知等差数列{an}的通项公式为an=f(n),则f(n)是关于n的一次函数
其中真命题的个数 为( )
A.1
B.2
C.3
D.4
【答案】分析:①若数列{an}是等差数列,且p+q=r(p,q,r为正整数)则ap+aq=ar,等差数列的性质判断;
②若数列{an}满足an+1=2an,则{an}是公比为2的等比数列,用用数列的类型来研究;
③2和8的等比中项为±4,用等比数列的性质判断;
④已知等差数列{an}的通项公式为an=f(n),则f(n)是关于n的一次函数,用数列的类型来判断.
解答:解:①若数列{an}是等差数列,且p+q=r(p,q,r为正整数)则ap+aq=ar,不是正确命题,应ap+aq=2ar.
②若数列{an}满足an+1=2an,则{an}是公比为2的等比数列,不是真命题,如:0,0,0,…
③2和8的等比中项为±4,正确,可由等比数列的性质证明出来.
④已知等差数列{an}的通项公式为an=f(n),则f(n)是关于n的一次函数不是真命题,如如:0,0,0,…
故选A
点评:本题考查命题真假判断与应用,求解此类题的关键是要对命题涉及的知识与定理、定义等有很好的理解与掌握.本题中举反例时易因为0,0,0,…太特殊了而想不到,学习时应该对各类数列进行分类归纳,明确其性质.
②若数列{an}满足an+1=2an,则{an}是公比为2的等比数列,用用数列的类型来研究;
③2和8的等比中项为±4,用等比数列的性质判断;
④已知等差数列{an}的通项公式为an=f(n),则f(n)是关于n的一次函数,用数列的类型来判断.
解答:解:①若数列{an}是等差数列,且p+q=r(p,q,r为正整数)则ap+aq=ar,不是正确命题,应ap+aq=2ar.
②若数列{an}满足an+1=2an,则{an}是公比为2的等比数列,不是真命题,如:0,0,0,…
③2和8的等比中项为±4,正确,可由等比数列的性质证明出来.
④已知等差数列{an}的通项公式为an=f(n),则f(n)是关于n的一次函数不是真命题,如如:0,0,0,…
故选A
点评:本题考查命题真假判断与应用,求解此类题的关键是要对命题涉及的知识与定理、定义等有很好的理解与掌握.本题中举反例时易因为0,0,0,…太特殊了而想不到,学习时应该对各类数列进行分类归纳,明确其性质.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
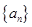 是等差数列,且
是等差数列,且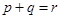 (
(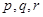 为正整数)则
为正整数)则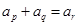
 是公比为2的等比数列
是公比为2的等比数列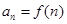 ,则
,则 是关于
是关于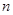 的一次函数
的一次函数