题目内容
设A是整数集的一个空子集,对于 如果
如果 且
且 那么称k是A的一个“孤立元”.给定
那么称k是A的一个“孤立元”.给定 由于S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
由于S的3个元素构成的所有集合中,不含“孤立元”的集合共有 个。
6
解析试题分析:依题意可知,没有与之相邻的元素是“孤立元”,因而无“孤立元”是指在集合中有与k相邻的元素.
因此,符合题意的集合是:{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,6,7},{6,7,8}共6个.
考点:新定义问题,阅读与理解、信息迁移及学生的学习潜力。
点评:中档题,关键是理解“没有与之相邻的元素是“孤立元”,因而无“孤立元”是指在集合中有与k相邻的元素“.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
已知集合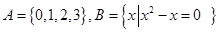 ,则集合
,则集合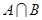 =( )
=( )
A.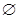 | B.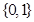 | C.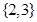 | D.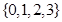 |
设 ,集合
,集合 ,则
,则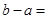 ( )
( )
| A.1 | B. | C.2 | D.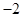 |
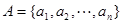 (n∈N*,n≥3),定义集合
(n∈N*,n≥3),定义集合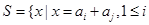
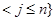 ,记集合S中的元素个数为S(A).(1)若集合A={1,2,3,4},则S(A)=______.
,记集合S中的元素个数为S(A).(1)若集合A={1,2,3,4},则S(A)=______. ,则
,则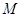 的所有非空真子集的个数是 .
的所有非空真子集的个数是 . ,
,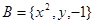 ,若
,若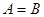 ,则
,则 .
.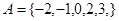 ,集合
,集合 ,集合
,集合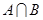 的真子集有 个.
的真子集有 个. ;②
;② ;③
;③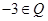 ;④
;④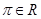 .
. ,集合
,集合 ,
, .
.
 ,若
,若 ,求实数
,求实数 的取值范围.
的取值范围.