题目内容

已知直线x-y+a=0与圆x²+y²=1交于A、B两点，且向量 $数学公式$ 、 $数学公式$ 满足| $数学公式$ + $数学公式$ |=| $数学公式$ - $数学公式$ |，其中O为坐标原点，则实数a的值为

A.
0
B.
-1
C.
1
D.
±1

D
分析：根据| $\text{[math]}$ + $\text{[math]}$ |=| $\text{[math]}$ - $\text{[math]}$ |，可知 $\text{[math]}$ ⊥ $\text{[math]}$ ，故圆心到直线的距离d= $\text{[math]}$ ，可求得a=±1．
解答：∵| $\text{[math]}$ + $\text{[math]}$ |=| $\text{[math]}$ - $\text{[math]}$ |，两边平方，得 $\text{[math]}$ • $\text{[math]}$ =0，即 $\text{[math]}$ ⊥ $\text{[math]}$ ．
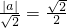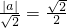故圆心（0，0）到直线x-y+a=0的距离d= $\text{[math]}$ ，求得a=±1．
故选D．
点评：本题考查了直线与圆相交的性质，熟练正确运用已知条件以及点到直线的距离是解决此问题的关键．

练习册系列答案

课课练与单元测试系列答案

世纪金榜小博士单元期末一卷通系列答案

单元测试AB卷台海出版社系列答案

黄冈新思维培优考王单元加期末卷系列答案

名校名师夺冠金卷系列答案

小学英语课时练系列答案

培优新帮手系列答案

天天向上一本好卷系列答案

小学生10分钟应用题系列答案

课堂作业广西教育出版社系列答案

相关题目

已知直线x+y=a与圆x²+y²=4交于A、B两点，且|

|，其中O为原点，则实数a的值为（　　）

已知直线x+y=a与圆x²+y²=4交于A、B两点，且

=2（其中O为原点），则实数a等于（　　）

已知直线x+y=a与圆x²+y²=4交于A、B两点，且|

|，其中O为原点，则实数a=

已知直线x+y=a与圆x²+y²=4交于A，B两点，O为原点，且

=2，则实数a的值等于

已知直线x+y+a=0与圆x²+y²-4x+4y+6=0有交点，则实数a的取值范围是（　　）

B．（-2，2）

D．（-∞，-2]∪[2，+∞）