题目内容
以下有关线性回归分析的说法不正确的是( )
A.通过最小二乘法得到的线性回归直线经过样本的中心 |
B.用最小二乘法求回归直线方程,是寻求使 最小的a,b的值 最小的a,b的值 |
| C.在回归分析中,变量间的关系若是非确定性关系,但因变量也能由自变量唯一确定 |
| D.如果回归系数是负的,y的值随x的增大而减小 |
C
解析试题分析:根据题意,那么回归分析中,通过最小二乘法得到的线性回归直线经过样本的中心 成立对于用最小二乘法求回归直线方程,是寻求使
成立对于用最小二乘法求回归直线方程,是寻求使 最小的a,b的值满足成立,对于如果回归系数是负的,y的值随x的增大而减小,类似于斜率为负数,成立排除法选C.具有相关关系的两个变量不一定是因果关系,因此选C.
最小的a,b的值满足成立,对于如果回归系数是负的,y的值随x的增大而减小,类似于斜率为负数,成立排除法选C.具有相关关系的两个变量不一定是因果关系,因此选C.
考点:回归方程
点评:本题考查两个变量的线性相关,考查线性相关关系的意义,考查散点图和线性回归方程的作用,本题是一个概念辨析问题.

练习册系列答案
相关题目
对变量x, y 有观测数据( ,
, )(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据(
)(i=1,2,…,10),得散点图1;对变量u ,v 有观测数据( ,
, )(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。
)(i=1,2,…,10),得散点图2. 由这两个散点图可以判断。 
图1 图2
| A.变量x 与y 正相关,u 与v 正相关 |
| B.变量x 与y 正相关,u 与v 负相关 |
| C.变量x 与y 负相关,u 与v 正相关 |
| D.变量x 与y 负相关,u 与v 负相关 |
有20位同学,编号从1至20,现在从中抽取4人作问卷调查,用系统抽样方法所确定的编号有可能是( ).
| A.3, 8,13,18 | B. 2,6,10,14 | C. 2,4,6,8 | D. 5,8,11,14 |
右表是某厂1~4月份用水量(单位:百吨)的一组数据:由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归直线方程是 ,则a等于( ).
,则a等于( ).
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 5.5 | 5 | 4 | 3.5 |
在一次对“学生的数学成绩与物理成绩是否有关”的独立性检验的试验中,由 列联表算得
列联表算得 的观测值
的观测值 ,参照附表:
,参照附表:
 | 0.050 | 0.010 | 0.001 |
 | 3.841 | 6.635 | 10.828 |
判断在此次试验中,下列结论正确的是( )
A. 有99.9%以上的把握认为“数学成绩与物理成绩有关”
B. “数学成绩与物理成绩有关” 的概率为99%
C. 在犯错误的概率不超过0.01的前提下,认为“数学成绩与物理成绩有关”
D. 在犯错误的概率不超过0.001的前提下,认为“数学成绩与物理成绩有关”
某交警部门对城区上下班交通情况作抽样调查,上下班时间各抽取12辆机动车的行驶速度(单位:km/h)作为样本进行研究,做出样本的茎叶图,则上班、下班时间行驶速度的中位数分别是( )
| A.28 27.5 | B.28 28.5 |
| C.29 27.5 | D.29 28.5 |
设有一个回归方程为 ,变量
,变量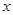 增加一个单位时,则
增加一个单位时,则
A.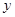 平均增加 平均增加 个单位 个单位 | B.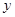 平均增加2个单位 平均增加2个单位 |
C.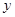 平均减少 平均减少 个单位 个单位 | D. 平均减少2个单位 平均减少2个单位 |
设有一个回归方程为y=2-3x,变量x增加1个单位时,则y平均( )
| A.增加2个单位 | B.减少2个单位 | C.增加3个单位 | D.减少3个单位 |
从总数为N的一批零件中抽取一个容量为30的样本,若每个零件被抽取的可能性为25%,则N为( )
| A.150 | B.200 | C.100 | D.120 |