题目内容
【题目】下列四个函数：①y=3﹣x；② 
；③y=x2+2x﹣10；④ 
，其中值域为R的函数有（ ）
A.1个
B.2个
C.3个
D.4个
【答案】B
【解析】解：根据一次函数的值域为R，y=3﹣x为一次函数，故①满足条件；
根据x2+1≥1，可得 
，即函数 
的值域为（0，1]，故②不满足条件；
二次函数y=x2+2x﹣10的最小值为﹣11，无最大值，故函数y=x2+2x﹣10的值域为[﹣11，+∞），故③不满足条件；
当x≤0时，y=﹣x≥0，当x＞0时，y=﹣ 
＜0，故函数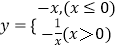 
的值域为R，故④满足条件；
故选B
【考点精析】解答此题的关键在于理解函数的值域的相关知识，掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
