题目内容
已知直线l:2x+y+2=0及圆C:x2+y2=2y.
(1)求垂直于直线l且与圆C相切的直线l′的方程;
(2)过直线l上的动点P作圆C的一条切线,设切点为T,求|PT|的最小值.
(1)求垂直于直线l且与圆C相切的直线l′的方程;
(2)过直线l上的动点P作圆C的一条切线,设切点为T,求|PT|的最小值.
(1)x-2y+2±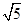 =0
=0
(2)
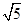 =0
=0(2)

(1)圆C的方程为x2+(y-1)2=1,其圆心为C(0,1),半径r=1.
由题意可设直线l′的方程为x-2y+m=0.
由直线与圆相切可得C到直线l′的距离d=r,即 =1,解得m=2±
=1,解得m=2±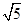 .
.
故直线l′的方程为x-2y+2±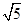 =0.
=0.
(2)结合图形可知:|PT|= =
= .故当|PC|最小时,|PT|有最小值.
.故当|PC|最小时,|PT|有最小值.
易知当PC⊥l时,|PC|取得最小值,且最小值即为C到直线l的距离,得|PC|min= .
.
所以|PT|min= =
= .
.
由题意可设直线l′的方程为x-2y+m=0.
由直线与圆相切可得C到直线l′的距离d=r,即
 =1,解得m=2±
=1,解得m=2±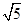 .
.故直线l′的方程为x-2y+2±
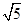 =0.
=0.(2)结合图形可知:|PT|=
 =
= .故当|PC|最小时,|PT|有最小值.
.故当|PC|最小时,|PT|有最小值.易知当PC⊥l时,|PC|取得最小值,且最小值即为C到直线l的距离,得|PC|min=
 .
.所以|PT|min=
 =
= .
.
练习册系列答案
 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
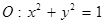 和点
和点 .
. 截得的弦长为8的圆M的方程;
截得的弦长为8的圆M的方程; 为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.
为定值?若存在,请求出定点R的坐标,并指出相应的定值;若不存在,请说明理由.

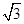 ,则直线l的方程为( )
,则直线l的方程为( )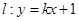 与圆
与圆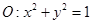 相交于
相交于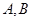 两点,则
两点,则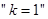 是“
是“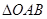 的面积为
的面积为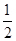 ”的( )
”的( ) 充分而不必要条件
充分而不必要条件  必要而不充分条件
必要而不充分条件 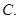 充分必要条件
充分必要条件 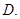 既不充分又不必要条件
既不充分又不必要条件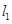 和
和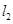 是圆
是圆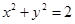 的两条切线,若
的两条切线,若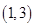 ,则
,则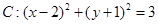 ,从点
,从点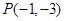 发出的光线,经
发出的光线,经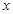 轴反射后恰好经过圆心
轴反射后恰好经过圆心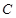 ,则入射光线的斜率为( )
,则入射光线的斜率为( )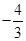



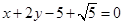 被圆
被圆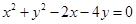 截得的弦长为 ( )
截得的弦长为 ( )