题目内容
由直线y=x,y=-x+1,及x轴围成平面图形的面积为
- A.∫01[(1-y)-y]dy
- B.∫0
 [(-x+1)-x]dx
[(-x+1)-x]dx - C.∫0
 [(1-y)-y]dy
[(1-y)-y]dy - D.∫01[(-x+1)-x]dx
C
分析:本题考查的定积分的简单应用,解决本题的关键是熟练进行图形的转换,掌握定积分几何意义,不难得到正确的答案.
解答: 解:如图,由直线y=x,y=-x+1,及x轴围成平面图形是红色的部分,
解:如图,由直线y=x,y=-x+1,及x轴围成平面图形是红色的部分,
它和图中蓝色部分的面积相同,
∵蓝色部分的面积S=∫0 [(1-x)-x]dx,
[(1-x)-x]dx,
即∫0 [(1-y)-y]dy.
[(1-y)-y]dy.
故选C.
点评:考查学生会利用导定积分几何意义,以及会利用定积分求图形面积的能力.定积分就是求函数F(X)在区间(a,b)中图线下包围 的面积.即 y=0 x=a x=b y=F(X)所包围的面积.
分析:本题考查的定积分的简单应用,解决本题的关键是熟练进行图形的转换,掌握定积分几何意义,不难得到正确的答案.
解答:
 解:如图,由直线y=x,y=-x+1,及x轴围成平面图形是红色的部分,
解:如图,由直线y=x,y=-x+1,及x轴围成平面图形是红色的部分,它和图中蓝色部分的面积相同,
∵蓝色部分的面积S=∫0
 [(1-x)-x]dx,
[(1-x)-x]dx,即∫0
 [(1-y)-y]dy.
[(1-y)-y]dy.故选C.
点评:考查学生会利用导定积分几何意义,以及会利用定积分求图形面积的能力.定积分就是求函数F(X)在区间(a,b)中图线下包围 的面积.即 y=0 x=a x=b y=F(X)所包围的面积.

练习册系列答案
 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
由直线y=x,y=-x+1,及x轴围成平面图形的面积为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
由直线y=x,y=-x+1,及x轴所围成的平面图形的面积可用定积分表示为( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
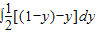

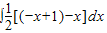

 [(-x+1)-x]d
[(-x+1)-x]d [(1-y)-y]dy
[(1-y)-y]dy