题目内容
已知△ABC中,cos2
=
(a,b,c分别是角A,B,C的对边)给出下列结论:
①
=1
②1<sinA+sinB+sinAsinB≤
+
;
③sin2A+cos2B=1;
④cos2A+cos2B=sin2C;
⑤tanA+tanB≥2.
其中正确的结论是
| A |
| 2 |
| b+c |
| 2c |
①
| tanA |
| tanB |
②1<sinA+sinB+sinAsinB≤
| 1 |
| 2 |
| 2 |
③sin2A+cos2B=1;
④cos2A+cos2B=sin2C;
⑤tanA+tanB≥2.
其中正确的结论是
②④⑤
②④⑤
(填写所有正确的结论编号)分析:利用降次升角公式,边角互化及勾股定理可得∠C=90°,进而逐一分析五个结论的真假,可得答案.
解答:解:∵cos2
=
∴
=
∴1+cosA=
+1
∴cosA=
∴
=
∴a2+b2=c2,
故∠C=90°
∴当A-B≠kπ,k∈Z时,等式
=1不成立,故①错误;
sinA+sinB+sinAsinB=sinA+cosA+sinAcosA=sinA+cosA+
令t=sinA+cosA,(0<A<90°),则1<t≤
令y=sinA+cosA+
=
t2+t-
=
(t+1)2-1,则y∈(1,
]
故②1<sinA+sinB+sinAsinB≤
+
正确;
sin2B≠cos2A时,等式sin2A+cos2B=sin2A+sin2B=1不成立,故③错误;
cos2A+cos2B=cos2A+sin2B=1=sin2C,故④正确;
tanA+tanB=tanA+
≥2,故⑤正确.
故正确的结论有:②④⑤
故答案为:②④⑤
| A |
| 2 |
| b+c |
| 2c |
∴
| 1+cosA |
| 2 |
| b+c |
| 2c |
∴1+cosA=
| b |
| c |
∴cosA=
| b |
| c |
∴
| b2+c2-a2 |
| 2bc |
| b |
| c |
∴a2+b2=c2,
故∠C=90°
∴当A-B≠kπ,k∈Z时,等式
| tanA |
| tanB |
sinA+sinB+sinAsinB=sinA+cosA+sinAcosA=sinA+cosA+
| (sinA+cosA)2-1 |
| 2 |
令t=sinA+cosA,(0<A<90°),则1<t≤
| 2 |
令y=sinA+cosA+
| (sinA+cosA)2-1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
故②1<sinA+sinB+sinAsinB≤
| 1 |
| 2 |
| 2 |
sin2B≠cos2A时,等式sin2A+cos2B=sin2A+sin2B=1不成立,故③错误;
cos2A+cos2B=cos2A+sin2B=1=sin2C,故④正确;
tanA+tanB=tanA+
| 1 |
| tanA |
故正确的结论有:②④⑤
故答案为:②④⑤
点评:本题以命题的真假判断为载体考查了三角函数的化简求值,其中熟练掌握正弦定理的推论“边角互化”是解答的关键.

练习册系列答案
相关题目
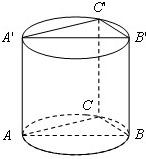 如图,直三棱柱ABC-A′B′C′内接于高为
如图,直三棱柱ABC-A′B′C′内接于高为 已知O是△ABC内任意一点,连接AO,BO,CO并延长交对边于A′,B′,C′,则
已知O是△ABC内任意一点,连接AO,BO,CO并延长交对边于A′,B′,C′,则 已知O是△ABC内任意一点,连结AO,BO,CO并延长交对边于A′,B′,C′,则
已知O是△ABC内任意一点,连结AO,BO,CO并延长交对边于A′,B′,C′,则