题目内容
已知a=(sin α,sin β),b=(cos(α-β),-1),c=(cos(α+β),2),α,β≠kπ+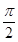 (k∈Z).
(k∈Z).
(1)若b∥c,求tan α·tan β的值;
(2)求a2+b·c的值.
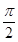 (k∈Z).
(k∈Z).(1)若b∥c,求tan α·tan β的值;
(2)求a2+b·c的值.
(1)-3(2)-1
(1)若b∥c,则2cos(α-β)+cos(α+β)=0,
∴3cos αcos β+sin αsin β=0,
∵α,β≠kπ+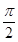 (k∈Z),∴tan αtan β=-3.
(k∈Z),∴tan αtan β=-3.
(2)a2+b·c=sin2α+sin2β+cos(α-β)cos(α+β)-2
=sin2α+sin2β+cos2αcos2β-sin2αsin2β-2
=sin2α+cos2αsin2β+cos2αcos2β-2
=sin2α+cos2α-2=1-2=-1.
∴3cos αcos β+sin αsin β=0,
∵α,β≠kπ+
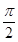 (k∈Z),∴tan αtan β=-3.
(k∈Z),∴tan αtan β=-3.(2)a2+b·c=sin2α+sin2β+cos(α-β)cos(α+β)-2
=sin2α+sin2β+cos2αcos2β-sin2αsin2β-2
=sin2α+cos2αsin2β+cos2αcos2β-2
=sin2α+cos2α-2=1-2=-1.

练习册系列答案
相关题目
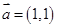 ,
,  ,
, ,则
,则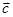 等于( )
等于( )
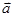 +
+


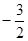

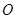 为坐标原点,直线
为坐标原点,直线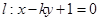 与圆
与圆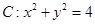 相交于
相交于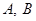 两点,
两点,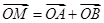 .若点
.若点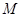 在圆
在圆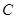 上,则实数
上,则实数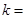 ( )
( )
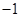

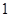
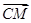 =3
=3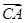 ,
,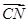 =2
=2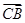 ,求点M、N及
,求点M、N及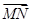 的坐标.
的坐标.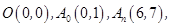 点
点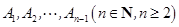 是线段
是线段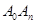 的
的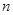 等分点,则
等分点,则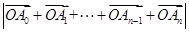 等于 .
等于 .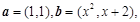 若
若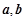 共线,则实数
共线,则实数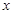 的值为( )
的值为( )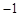
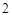
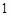 或
或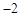
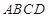 的边长为
的边长为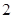 ,
,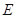 为
为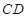 的中点,则
的中点,则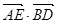 = ( )
= ( )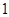
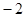
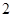
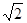
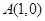 ,
,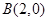 ,若动点
,若动点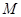 满足
满足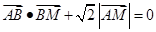 ,则点
,则点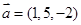 ,
,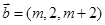 ,若
,若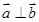 ,则
,则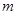 的值为 .
的值为 .