题目内容
 中内角
中内角 的对边分别为
的对边分别为 ,向量
,向量 且
且 (1)求锐角
(1)求锐角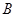 的大小;(2)如果
的大小;(2)如果 ,求
,求 的面积
的面积 的最大值
的最大值解:(1)
(2) (当且仅当
(当且仅当  时等号成立。)
时等号成立。)

(2)
 (当且仅当
(当且仅当  时等号成立。)
时等号成立。)本试题主要是考查了向量的共线以及三角函数中的二倍角公式的运用,以及余弦定理和三角形面积公式的求解的综合运用。
(1)因为向量平行,可知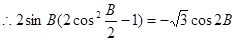
,然后利用二倍角公式化简可知角B的值。
(2)由余弦定理得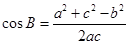 结合上一问的结论可知
结合上一问的结论可知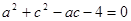 ,结合均值不等式求得最值。
,结合均值不等式求得最值。
解:(1)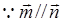
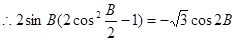
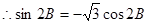 即
即 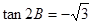
又 为锐角
为锐角 

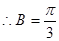
(2) 由余弦定理得
由余弦定理得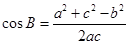
即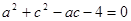
又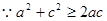 代入上式得
代入上式得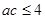 (当且仅当
(当且仅当  时等号成立)
时等号成立)
 (当且仅当
(当且仅当  时等号成立。)
时等号成立。)
(1)因为向量平行,可知
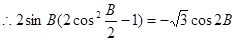
,然后利用二倍角公式化简可知角B的值。
(2)由余弦定理得
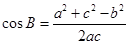 结合上一问的结论可知
结合上一问的结论可知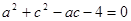 ,结合均值不等式求得最值。
,结合均值不等式求得最值。解:(1)
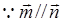
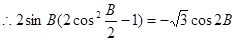
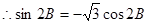 即
即 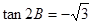
又
 为锐角
为锐角 

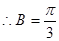
(2)
 由余弦定理得
由余弦定理得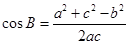
即
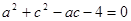
又
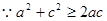 代入上式得
代入上式得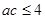 (当且仅当
(当且仅当  时等号成立)
时等号成立) (当且仅当
(当且仅当  时等号成立。)
时等号成立。)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (定值),半径为
(定值),半径为 (定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为
(定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为 ,则按图二作出的矩形面积的最大值为_____________.
,则按图二作出的矩形面积的最大值为_____________.
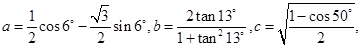 则有( )
则有( )
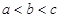
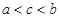
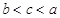
 的值是 。
的值是 。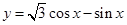 的最大值是 .
的最大值是 .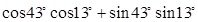 的值( )
的值( )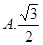


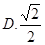
 ,则
,则 = .
= . 则
则 的值为________________.
的值为________________.