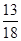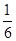题目内容
已知扇形的圆心角为 (定值),半径为
(定值),半径为 (定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为
(定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为 ,则按图二作出的矩形面积的最大值为_____________.
,则按图二作出的矩形面积的最大值为_____________.
 (定值),半径为
(定值),半径为 (定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为
(定值),分别按图一、二作扇形的内接矩形,若按图一作出的矩形面积的最大值为 ,则按图二作出的矩形面积的最大值为_____________.
,则按图二作出的矩形面积的最大值为_____________.
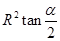
解:图一,设∠MOQ=x,则MQ=rsinx
在△OMN中,MN /sin(2α-x) ="r" /sin(180°-2α) ,∴MN=rsin(2α-x) /sin2α
∴矩形面积S=r2sin(2α-x) sinx/ sin2α =r2 2sin2α [cos(2x-2α)-cos2α]≤r2 2sin2α [1-cos2α]="1" /2 r2tanα
当且仅当x=α时,取得最大值,故图一矩形面积的最大值为1 2 r2tanθ,图二可拆分成两个,
图一角是2α,图二拆分后角是α,故根据图1得出的结论,可得矩形面积的最大值为
1/ 2 r2tan(θ/2)而图二时由两个这样的图形组成,所以两个则为r2tan(θ/ 2 ).
故答案为:r2tan(θ/2)
在△OMN中,MN /sin(2α-x) ="r" /sin(180°-2α) ,∴MN=rsin(2α-x) /sin2α
∴矩形面积S=r2sin(2α-x) sinx/ sin2α =r2 2sin2α [cos(2x-2α)-cos2α]≤r2 2sin2α [1-cos2α]="1" /2 r2tanα
当且仅当x=α时,取得最大值,故图一矩形面积的最大值为1 2 r2tanθ,图二可拆分成两个,
图一角是2α,图二拆分后角是α,故根据图1得出的结论,可得矩形面积的最大值为
1/ 2 r2tan(θ/2)而图二时由两个这样的图形组成,所以两个则为r2tan(θ/ 2 ).
故答案为:r2tan(θ/2)

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 中内角
中内角 的对边分别为
的对边分别为 ,向量
,向量 且
且 (1)求锐角
(1)求锐角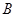 的大小;(2)如果
的大小;(2)如果 ,求
,求 的最大值
的最大值
 时,求
时,求 的值;
的值; 在
在 上的值域.
上的值域. ,若
,若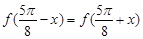 ,那么
,那么 等于 .
等于 . 则
则 等于( )
等于( )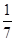
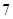


 ,
,  ,则
,则
 =
=  的值为
的值为  的值是( )
的值是( )