题目内容
函数 的最小值为( )
的最小值为( )
A. | B.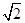 | C.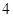 | D. |
A
解析试题分析:根据绝对值不等式的放缩,根据绝对值的和大于等于差的绝对值 可知结论。解: 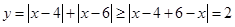 ,故答案为A.
,故答案为A.
考点:绝对值不等式
点评:主要是考查了运用绝对值不等式来求解最值的运用,属于基础题。

练习册系列答案
相关题目
若集合 ,则实数a的取值范围是
,则实数a的取值范围是
A.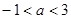 | B.1<a<4 | C.0<a<3 | D.0<a<4 |
不等式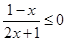 的解集为( )
的解集为( )
A.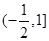 | B. |
C.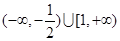 | D.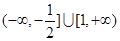 |
要使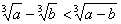 成立,则
成立,则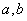 应满足的条件是
应满足的条件是
A.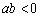 且 且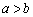 | B.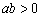 且 且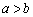 |
C.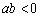 且 且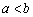 | D.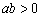 且 且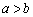 或 或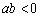 且 且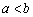 |
不等式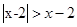 的解集是( )
的解集是( )
A.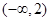 | B.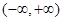 | C.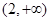 | D.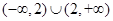 |
二次不等式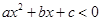 的解集是全体实数的条件是( )
的解集是全体实数的条件是( )
A.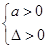 | B. | C.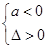 | D.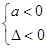 |
若不等式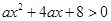 的解集为
的解集为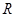 ,则实数
,则实数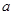 的取值范围是
的取值范围是
A.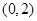 | B.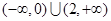 |
C.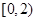 | D.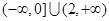 |
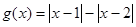 ,则
,则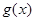 的值域为 ;若关于
的值域为 ;若关于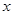 的不等式
的不等式 的解集为空集,则实数
的解集为空集,则实数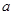 的取值范围是 .
的取值范围是 .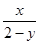 ,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )
,若关于x的不等式(x-a)⊙(x+1-a)>0的解集是集合{x|-2≤x≤2,x∈R}的子集,则实数a的取值范围是( )