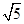题目内容
已知 ,
, 是双曲线
是双曲线 的左,右焦点,若双曲线左支上存在一点
的左,右焦点,若双曲线左支上存在一点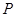 与点
与点 关于直线
关于直线 对称,则该双曲线的离心率为
对称,则该双曲线的离心率为
A.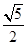 | B. | C.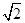 | D. |
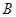
解析试题分析: 即双曲线的一条渐近线方程.过焦点
即双曲线的一条渐近线方程.过焦点 且垂直渐近线的直线方程为:
且垂直渐近线的直线方程为: ,与
,与 联立,解之可得
联立,解之可得
故对称中心的点坐标为( );
);
由中点坐标公式可得对称点的坐标为 ,将其代入双曲线的方程可得
,将其代入双曲线的方程可得 结合
结合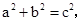
化简可得 ,故
,故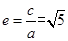 .故选
.故选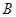 .
.
考点:双曲线的几何性质,直线方程,两直线的位置关系.

练习册系列答案
相关题目
若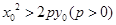 ,则称点
,则称点 在抛物线C:
在抛物线C: 外.已知点
外.已知点 在抛物线C:
在抛物线C: 外,则直线
外,则直线 与抛物线C的位置关系是( )
与抛物线C的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.不能确定 |
若椭圆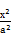 +
+ =1(a>b>0)的离心率为
=1(a>b>0)的离心率为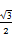 ,则双曲线
,则双曲线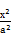 -
- =1的渐近线方程为( )
=1的渐近线方程为( )
A.y=± x x | B.y=±2x |
| C.y=±4x | D.y=± x x |
已知双曲线C的中心在原点,焦点在坐标轴上,P(1,-2)是C上的点,且y=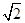 x是C的一条渐近线,则C的方程为( )
x是C的一条渐近线,则C的方程为( )
A. -x2=1 -x2=1 |
B.2x2- =1 =1 |
C. -x2=1或2x2- -x2=1或2x2- =1 =1 |
D. -x2=1或x2- -x2=1或x2- =1 =1 |
抛物线y=ax2的准线方程是y=2,则a的值为( )
A. | B. | C.8 | D.﹣8 |
已知双曲线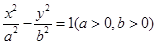 的两条渐近线均与
的两条渐近线均与 相切,则该双曲线离心率等于( )
相切,则该双曲线离心率等于( )
A. | B. | C.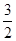 | D. |
 ,它们所表示的曲线可能是( )
,它们所表示的曲线可能是( )
 为C的实轴长的2倍,则C的离心率为
为C的实轴长的2倍,则C的离心率为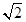

 =1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率等于( )
=1(a>0,b>0)的渐近线与抛物线y=x2+1相切,则该双曲线的离心率等于( )