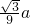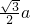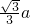题目内容
平面α内有∠BOC=60°,OA是平面α的斜线段,且OA=a,OA与∠BOC的两边所成的角都是45°,那么点A到平面α的距离是( )
分析:设点A在平面α的射影是H,作HE⊥OB,垂足为E,作HF⊥OC 垂足为F,证得Rt△AE0≌Rt△AFO 得出OE=OF=
a,,从而又得Rt△HEO≌Rt△HFO,得出,OH=
a,最后在RtAHO中应用勾股定理解出AH.
| ||
| 2 |
| ||
| 3 |
解答: 解:设点A在平面α的射影是H,则AH为所求,作HE⊥OB,垂足为E,则OB⊥面AEH,
解:设点A在平面α的射影是H,则AH为所求,作HE⊥OB,垂足为E,则OB⊥面AEH,
∴OB⊥AE,同理作 HF⊥OC,∴OC⊥AF.
∴Rt△AE0≌Rt△AFO∴OE=OF,从而又得Rt△HEO≌Rt△HFO,∴∠EOH=∠FOH=30°
.在Rt△AE0中,OE=AO•sin∠AOB=
a,
在Rt△HEO中,OE=OH•cos∠EOH,∴OH=
a
在RtAHO中,AH2=AO2-OH2=a2-
a2=
a2∴AH=
a.
故选D.
 解:设点A在平面α的射影是H,则AH为所求,作HE⊥OB,垂足为E,则OB⊥面AEH,
解:设点A在平面α的射影是H,则AH为所求,作HE⊥OB,垂足为E,则OB⊥面AEH,∴OB⊥AE,同理作 HF⊥OC,∴OC⊥AF.
∴Rt△AE0≌Rt△AFO∴OE=OF,从而又得Rt△HEO≌Rt△HFO,∴∠EOH=∠FOH=30°
.在Rt△AE0中,OE=AO•sin∠AOB=
| ||
| 2 |
在Rt△HEO中,OE=OH•cos∠EOH,∴OH=
| ||
| 3 |
在RtAHO中,AH2=AO2-OH2=a2-
| 2 |
| 3 |
| 1 |
| 3 |
| ||
| 3 |
故选D.
点评:本题考查了直线与平面之间的位置关系,以及点面距离,考查空间想象能力、运算能力和推理论证能力.

练习册系列答案
相关题目
 ,D是A点在BC边上的射影,则
,D是A点在BC边上的射影,则 .”。拓展到空间,若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,点O是顶点A在底面BCD上的射影且O点在△BCD内,类比平面上三角形的射影定理,△ABC、△BOC、△BCD三者的面积关系是
.”。拓展到空间,若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,点O是顶点A在底面BCD上的射影且O点在△BCD内,类比平面上三角形的射影定理,△ABC、△BOC、△BCD三者的面积关系是