题目内容
方程（a2+1）x2-2ax-3=0的两根x1，x2满足|x2|＜x1（1-x2）且0＜x1＜1，则实数a的取值范围是（ ）
A、（1，
| ||||||
B、（1+
| ||||||
C、（-
| ||||||
D、（-
|
分析：根据方程根的个数与判别式之间的关系证明△＞0恒成立，由题意判断出另一个根的范围，再由f（1）＞0求出a的范围，利用f（0）＜0进一步确定两个根的关系，再由韦达定理求出a范围，再取交集．
解答：解：∵|x2|＜x1（1-x2），∴x1（1-x2）＞0，又∵0＜x1＜1，∴x2＜1
设f（x）=（a2+1）x2-2ax-3，∵方程有两根，∴△=4a2+12（a2+1）＞0恒成立，
则f（1）=a2-2a-2＞0，解得a＞1+
或a＜1-
；
∵f（0）=-3，∴x2＜0＜x1＜1，
则|x2|＜x1（1-x2）可化简为：x1+x2＞x1x2，利用韦达定理得
＞-
解得a＞-
．
∴实数a的取值范围是：（-
，1-
）∪（1+
，+∞）
故选C．
设f（x）=（a2+1）x2-2ax-3，∵方程有两根，∴△=4a2+12（a2+1）＞0恒成立，
则f（1）=a2-2a-2＞0，解得a＞1+
| 3 |
| 3 |
∵f（0）=-3，∴x2＜0＜x1＜1，
则|x2|＜x1（1-x2）可化简为：x1+x2＞x1x2，利用韦达定理得
| 2a |
| a2+1 |
| 3 |
| a2+1 |
解得a＞-
| 3 |
| 2 |
∴实数a的取值范围是：（-
| 3 |
| 2 |
| 3 |
| 3 |
故选C．
点评：本题考查了一元二次方程的解法，对于含有参数的方程，借助于判别式的符号以及韦达定理、根的范围对应的函数值的符号，进行求解．
练习册系列答案
小题狂做系列答案
相关题目
）
，+∞）
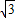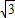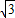，1-
）∪（1+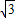
，+∞）
，+∞）