题目内容
已知复数z=bi(b∈R),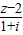 是实数,i是虚数单位.
是实数,i是虚数单位.(1)求复数z;
(2)若复数(m+z)2所表示的点在第一象限,求实数m的取值范围.
【答案】分析:(1)由z=bi(b∈R),化简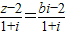 为
为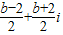 .根据
.根据 是实数,可得
是实数,可得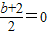 ,求得 b的值,可得z的值.
,求得 b的值,可得z的值.
(2)化简 (m+z)2为 (m2-4)-4mi,根据复数f(4)所表示的点在第一象限,可得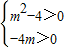 ,解不等式组求得实数m的取值范围.
,解不等式组求得实数m的取值范围.
解答:解:(1)∵z=bi(b∈R),∴ =
=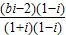 =
= =
=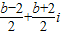 .
.
又∵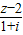 是实数,∴
是实数,∴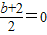 ,
,
∴b=-2,即z=-2i.
(2)∵z=-2i,m∈R,∴(m+z)2=(m-2i)2=m2-4mi+4i2=(m2-4)-4mi,
又∵复数f(4)所表示的点在第一象限,∴ ,…(10分)
,…(10分)
解得m<-2,即m∈(-∞,-2)时,复数f(4)所表示的点在第一象限.
点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,虚数单位i的幂运算性质,属于基础题.
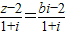 为
为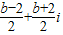 .根据
.根据 是实数,可得
是实数,可得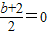 ,求得 b的值,可得z的值.
,求得 b的值,可得z的值.(2)化简 (m+z)2为 (m2-4)-4mi,根据复数f(4)所表示的点在第一象限,可得
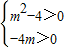 ,解不等式组求得实数m的取值范围.
,解不等式组求得实数m的取值范围.解答:解:(1)∵z=bi(b∈R),∴
 =
=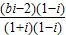 =
= =
=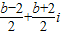 .
.又∵
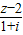 是实数,∴
是实数,∴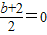 ,
,∴b=-2,即z=-2i.
(2)∵z=-2i,m∈R,∴(m+z)2=(m-2i)2=m2-4mi+4i2=(m2-4)-4mi,
又∵复数f(4)所表示的点在第一象限,∴
 ,…(10分)
,…(10分)解得m<-2,即m∈(-∞,-2)时,复数f(4)所表示的点在第一象限.
点评:本题主要考查复数的基本概念,两个复数代数形式的乘除法法则的应用,虚数单位i的幂运算性质,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目