题目内容
已知:向量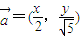 ,
,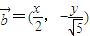 ,曲线
,曲线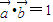 上一点P到点F(3,0)的距离为6,M为PF的中点,O为坐标原点,则|OM|=( )
上一点P到点F(3,0)的距离为6,M为PF的中点,O为坐标原点,则|OM|=( )A.1
B.2
C.5
D.1或5
【答案】分析:由数量积的运算易得方程为双曲线,由双曲线的定义结合三角形的中位线的性质,易得答案.
解答:解:∵向量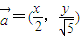 ,
,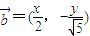 ,
,
∴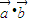 =
=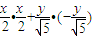 =
=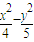 =1,
=1,
对应的图形是双曲线,其中a2=4,b2=5,故a=2,b= ,c=
,c=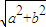 =3,
=3,
可得点F(3,0)恰好是双曲线的右焦点,
设双曲线的左焦点为F'(-3,0),连接PF'、OM
由双曲线的定义可得|PF-PF'|=|6-PF'|=2a=4,
解得PF'=2或10,
∵OM是△PFF'的中位线,∴|OM|= PF'=1或5,
PF'=1或5,
故选D
点评:本题考查平面向量的数量积的运算,涉及双曲线的定义,属基础题.
解答:解:∵向量
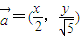 ,
,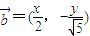 ,
,∴
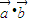 =
=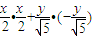 =
=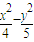 =1,
=1,对应的图形是双曲线,其中a2=4,b2=5,故a=2,b=
 ,c=
,c=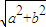 =3,
=3,可得点F(3,0)恰好是双曲线的右焦点,
设双曲线的左焦点为F'(-3,0),连接PF'、OM
由双曲线的定义可得|PF-PF'|=|6-PF'|=2a=4,
解得PF'=2或10,
∵OM是△PFF'的中位线,∴|OM|=
 PF'=1或5,
PF'=1或5,故选D
点评:本题考查平面向量的数量积的运算,涉及双曲线的定义,属基础题.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
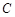 :
: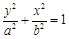
 过点
过点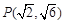 ,上、下焦点分别为
,上、下焦点分别为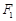 、
、 ,
,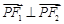 .直线
.直线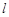 与椭圆交于
与椭圆交于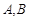 两点,线段
两点,线段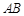 中点为
中点为 .
.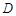 ,若曲线
,若曲线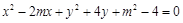 与区域
与区域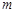 的最小值.
的最小值.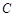 :
: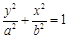
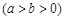 过点
过点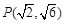 ,上、下焦点分别为
,上、下焦点分别为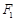 、
、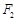 ,
,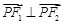 .直线
.直线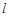 与椭圆交于
与椭圆交于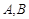 两点,线段
两点,线段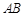 中点为
中点为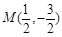 .
.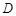 ,若曲线
,若曲线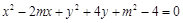 与区域
与区域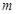 的最小值.
的最小值.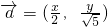 ,
,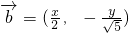 ,曲线
,曲线 上一点P到点F(3,0)的距离为6,M为PF的中点,O为坐标原点,则|OM|=
上一点P到点F(3,0)的距离为6,M为PF的中点,O为坐标原点,则|OM|=